Oberflächen modellieren
![]()
![]()
![]()
Einführung
Eine Oberfläche ist eine einseitige Darstellung der Außenseite eines Bauteils, die weder eine Masse noch eine Dicke hat.
Bei der Oberflächenmodellierung handelt es sich um einen Modellierungsansatz, der es Konstrukteuren ermöglicht, komplexe geometrische Merkmale und organische Formen zu erstellen, die mit Volumen-Tools zum Modellieren allein nicht erzeugt werden können. Die Oberflächenmodellierung wird für eher für freiere Formen und Features verwendet als die Modellierung von Volumenkörpern.
Beispielsweise kann ein Würfel-Volumenkörper in sechs verschiedene Flächen aufgeteilt werden. Jede Fläche stellt eine Oberfläche dar, die den Volumenkörper umschließt und so den Würfel bildet. Bei der Oberflächengestaltung können Sie jede Seite des Würfels als einzelne Oberfläche erstellen. Wenn alle sechs Seiten des Würfels erstellt wurden, werden die Oberflächen zu einem Volumen addiert, das einen Volumenkörper bildet.
Dafür wird Oberflächengeometrie verwendet:
-
Volumenkörper erstellen:
-
Mit der Funktion „Verdicken“ wird eine Oberfläche verdickt, sodass ein Volumenkörper entsteht.
-
Mithilfe der Funktion „Umschließen“ wird ein Volumenkörper erzeugt, indem ein geschlossenes Volumen gebildet wird, bei dem jede Kante zwei Flächen begrenzt.
-
-
Sie können Konstruktionsgeometrie erstellen (Trennlinien für Formen, Verschmelzung und Überbrückung der Geometrie, Stützen für Ausformungen und Füllungen zur Anpassung von Krümmung und Tangentialität).
-
Ersetzen Sie die Fläche eines Volumenkörpers durch eine komplexere Geometrie (mithilfe des Features „Fläche ersetzen“).
Die Kontinuität von Kurven und Oberflächen ist ein Maß für die Glätte zwischen zwei Kurven oder zwei Oberflächen, an denen sie sich berühren. Wenn Kurven und Oberflächen zu geometrischen Modellen zusammengesetzt werden, wird Kontinuität immer wichtiger, um eine möglichst fließende oder kontinuierliche organische Form zu erzeugen.
Die Bezeichnung G (oder Geometrie) wird verwendet, um die Kurven-/Oberflächenkontinuität (G0 bis G3) zu bestimmen. In Onshape entsprechen diese Bezeichnungen den Optionen „Anpassen“ in vielen Kurven- und Oberflächen-Features (z. B. Brückenkurven, Verrundung, Flächenüberblendung u. ä.). Diese Klassifizierungen der Kontinuität werden im Folgenden zusammen mit ihren Definitionen beschrieben:
-
G0 (Position anpassen): Die Position wird zwischen den zwei Kurven/Oberflächen angepasst. Beide Kurven/Oberflächen haben eine gemeinsame Position am Gelenk.
-
G1 (Tangente anpassen): Die Tangente wird zwischen den zwei Kurven/Oberflächen angepasst. Beide Kurven/Oberflächen berühren sich und haben einen gemeinsamen Winkel, der an beiden Enden gleich ist. Eine Verrundung ist ein gutes Beispiel für diese Art der Kontinuitätsanpassung.
-
G2 (Krümmung anpassen): Die Krümmung (Radius) wird zwischen den zwei Kurven/Oberflächen angepasst. Beide Kurven/Oberflächen berühren sich, sind tangential und haben an dem Punkt, an dem sie sich berühren, dieselbe Krümmung (beide haben identische Radien).
-
G3 (Fluss anpassen): Der Fluss wird zwischen den zwei Kurven/Oberflächen angepasst. Beide Kurven/Oberflächen berühren sich, sind tangential, haben eine ähnliche Krümmung und zeigen das Ausmaß der Krümmungsänderung über die Länge der Krümmung (Fluss).
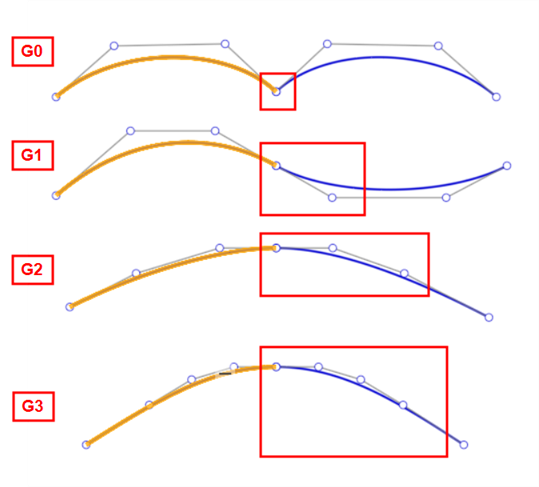
Mithilfe der Funktion Brückenkurve können Sie eine Brückenkurve (unten orange dargestellt) zwischen zwei Kurven erstellen und deren Start- und Endposition, Tangente, Krümmung und Fluss anpassen (oder eine Kombination aus beiden, z. B. Position am Anfang anpassen und Krümmung am Ende anpassen):
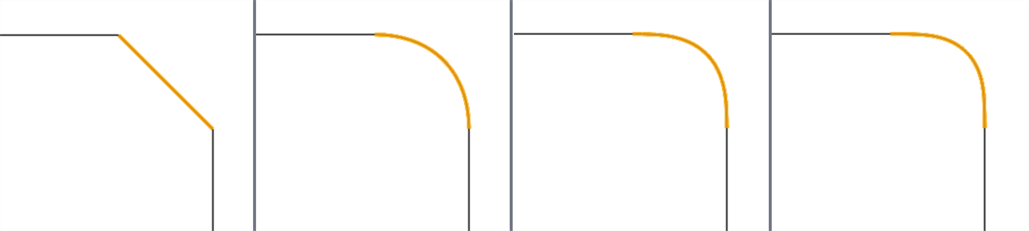
Von links nach rechts: G0 (Position anpassen), G1 (Tangente anpassen), G2 (Krümmung anpassen), G3 (Fluss anpassen)
Wenn Sie dies über Kurven hinaus erweitern, können Sie eine Oberfläche zwischen zwei Oberfläche erstellen und ihre Start- und Endkontinuität auf die gleiche Weise anpassen:

Von links nach rechts: G0 (Position anpassen), G1 (Tangente anpassen), G2 (Krümmung anpassen), G3 (Fluss anpassen)
Wenn Sie die Kurven- oder Oberflächenkontinuität mit dem Kurven-/Oberflächenanalyse-Tool analysieren, können Sie feststellen, dass mit jeder progressiven Kontinuitätsanpassung die Verbindungen zwischen den Kurven/Flächen glatter werden und glattere Krümmungskämme entstehen. G0 (Position anpassen) kann mit der Kurven-/Oberflächenanalyse nicht analysiert werden, da eine gerade Linie keine Krümmung aufweist.
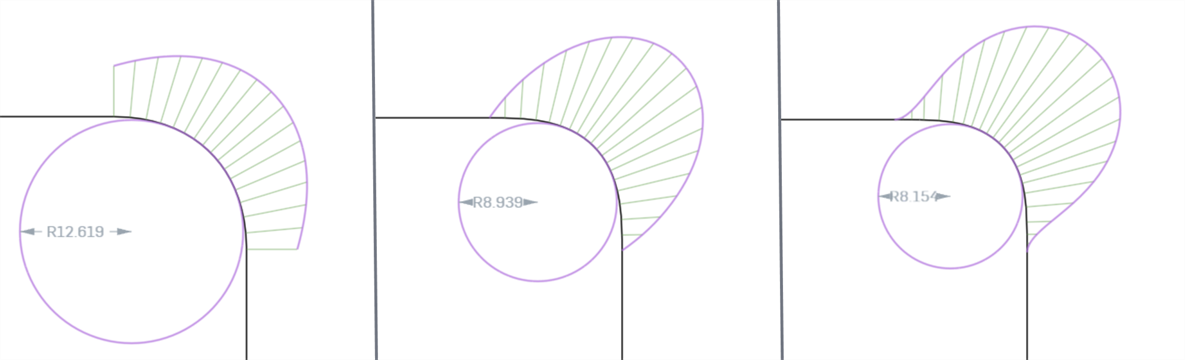
Von links nach rechts: G1 (Tangente anpassen), G2 (Krümmung anpassen), G3 (Fluss anpassen)
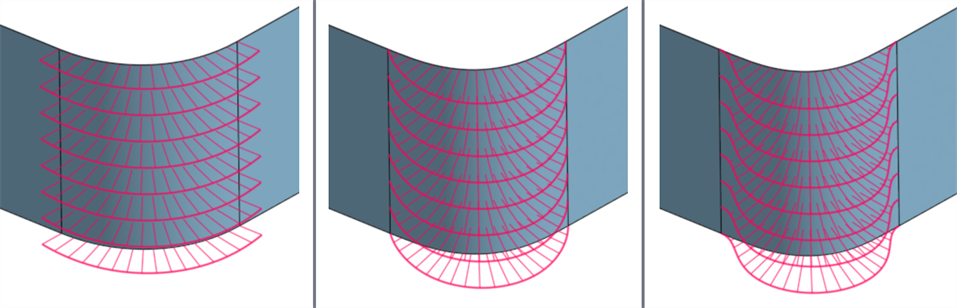
Von links nach rechts: G1 (Tangente anpassen), G2 (Krümmung anpassen), G3 (Fluss anpassen)
Wenn Sie die Kurven- oder Oberflächenkontinuität mit dem Zebrastreifen-Tool analysieren, wird die Verbindung zwischen den Kurven/Oberflächen mit jeder progressiven Kontinuitätsübereinstimmung glatter. Zebrastreifen an den Oberflächenkanten werden zunehmend glatter, je mehr Sie den Wert von G0 (Position anpassen) auf G2 (Kontinuität anpassen) erhöhen:

Von links nach rechts: G0 (keine Kontinuität), G1 (Tangente anpassen) und G2 (Krümmung anpassen)
Die folgenden Beispiele veranschaulichen die Kontinuitäten auf einer Brückenkurve zwischen zwei anderen nichtlinearen Kurven. Die Brückenkurve ist magentafarben. Die erste Spalte zeigt das Dialogfenster „Brückenkurve“ und die Auswahl der Kontinuität mit dem Ergebnis (und „Steuerpunkte bearbeiten“ aktiviert), die mittlere Spalte zeigt die Brückenkurve mit deaktivierter Option „Steuerpunkte bearbeiten“ und die letzte Spalte zeigt die Kurven-/Oberflächenanalyse für alle Kurven:
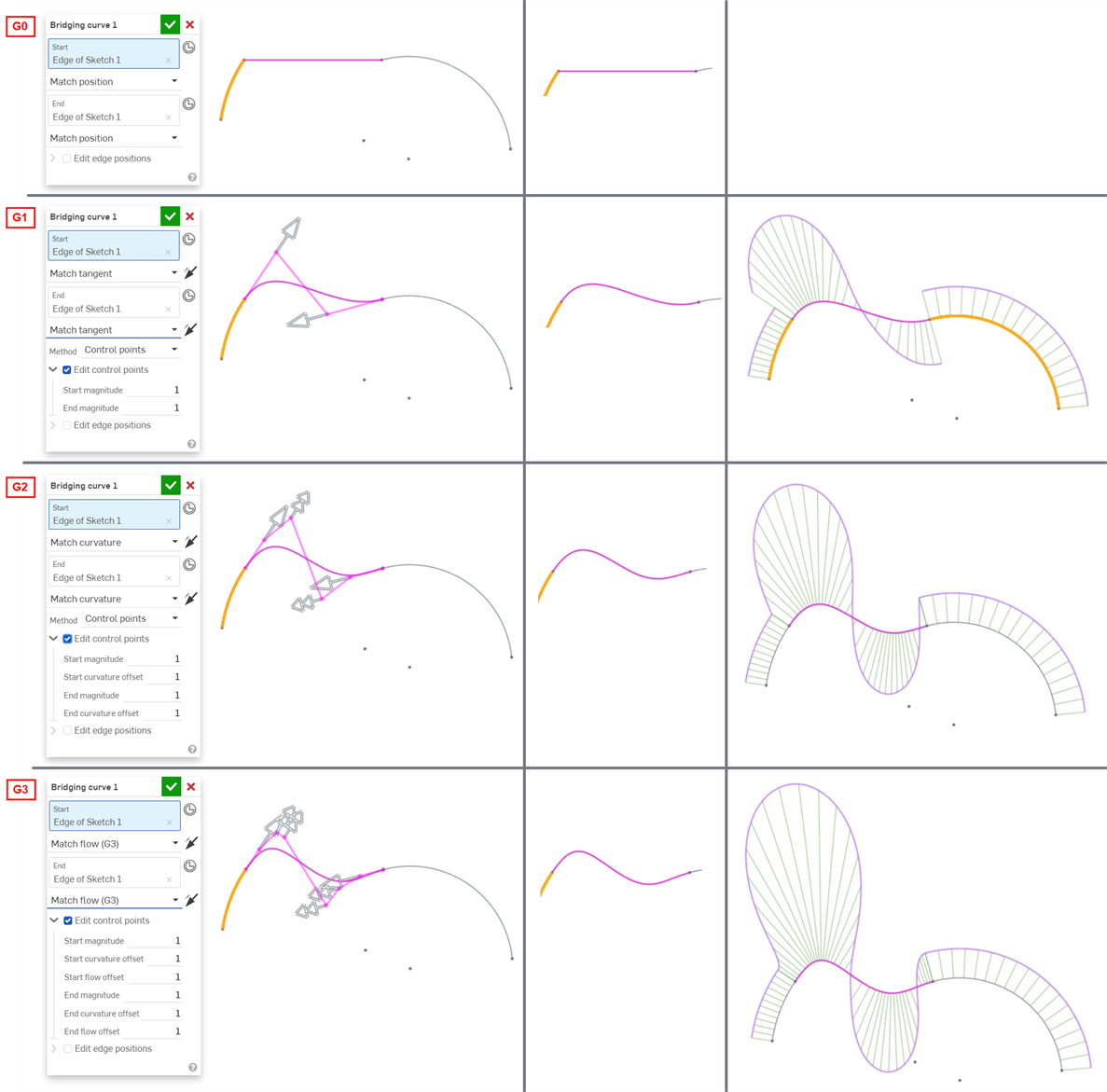
Die für die Kurven- und Flächenverbindungen in Ihrem Modell gewählte Kontinuität hängt ganz von der Kontinuität ab, die an jedem Knotenpunkt bzw. jeder Kante erforderlich ist. Es gibt keine richtige oder falsche Oberflächenkontinuität.
Darüber hinaus erfordern höhere Kontinuitätsgrade mehr Steuerpunkte zur Durchsetzung. G0 benötigt nur einen Steuerpunkt (den Endpunkt), G1 benötigt zwei, G2 benötigt drei und G3 benötigt vier. Eine Bezier-Kurve, die an beiden Enden durch G3 eingeschränkt ist, erfordert mindestens acht Steuerpunkte, vier für jedes Ende.
Beim Modellieren mit Oberflächen sind zusätzliche Schritte erforderlich, um hochwertige Oberflächen zu erstellen. Diese Schritte verbessern die Leistung, vermeiden Unvollkommenheiten und optimieren die Erstellung komplexer Oberflächen.
-
Kurven-/Oberflächenanalyse: Visualisieren und analysieren Sie die Krümmung auf einer Skizze im Part Studio. Rufen Sie das Dialogfenster „Kurven-/Oberflächenanalyse“ auf, indem Sie Umschalt+C drücken, mit der rechten Maustaste auf eine Skizze, ein Bauteil oder eine Fläche klicken oder auf das Symbol „Analyse-Tools anzeigen (
 ) in der unteren rechten Ecke der Benutzeroberfläche klicken.
) in der unteren rechten Ecke der Benutzeroberfläche klicken.Diese Tools zeigen Krümmungskämme (die Intensität der Krümmung an einem bestimmten Punkt entlang einer Kante oder Fläche) und Steuerpunkt-Raster an. Idealerweise sollten die Krümmungskämme eine stetige Zunahme oder Abnahme aufweisen.

Das folgende Beispiel sieht ohne Evaluierungs-Tools gut aus, zeigt aber bei eingeschalteter Krümmungs-/Oberflächenanalyse extreme Krümmungsschwankungen (vor allem in Richtung des roten U unten links). Besonders problematisch ist dabei die Außenkante (unten rechts):
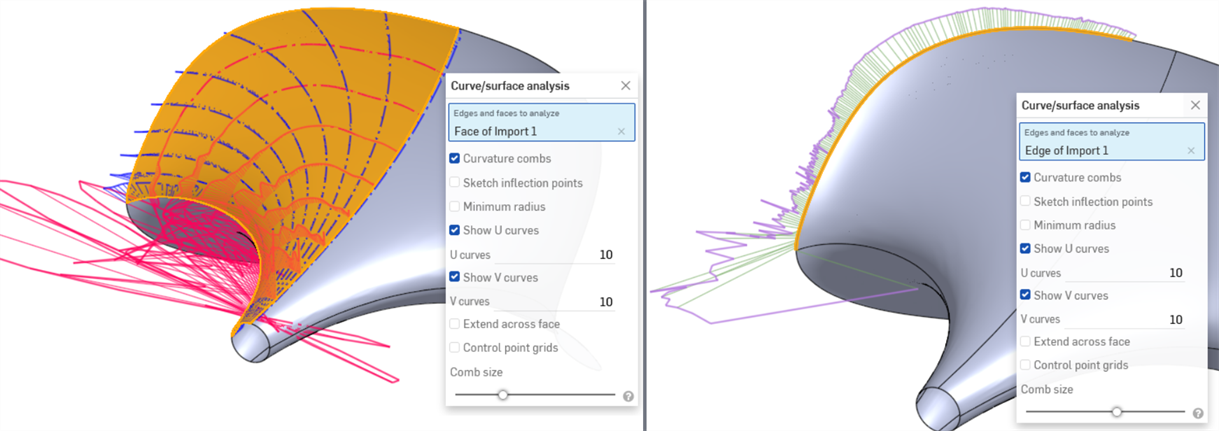
Darüber hinaus spiegelt das Steuerpunkt-Raster die Komplexität der Oberfläche wider. Verlauf und Dichte der Steuerpunkte können ein Modell mit zu vielen Steuerpunkten veranschaulichen:

-
Connection analysis - Assess or report the connection between curves and surfaces in a Part Studio or Sketch. Access the Connection analysis dialog from the Show analysis tools icon (
 ) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
-
Zebrastreifen und Farbkarte: Zebrastreifen stellen die Reflexion eines gestreiften Raums auf dem aktuellen Modell, den aktuellen Flächen oder Oberflächen in einem Part Studio oder einer Baugruppe dar. So können Sie erkennen, ob die Krümmung an Kanten und Flächen ausgerichtet und kontinuierlich ist. Der Zugriff auf Zebrastreifen erfolgt über das Symbol „Analyse-Tools anzeigen“ (
 ) in der unteren rechten Ecke der Benutzeroberfläche.
) in der unteren rechten Ecke der Benutzeroberfläche.Zebrastreifen stimmen nicht mit G0 oder der Positionskontinuität überein. Bei G1 oder der Tangentenkontinuität stimmen sie direkt an der Kante überein, weichen jedoch stark voneinander ab. Bei G2 oder der Krümmungskontinuität verlaufen die Zebrastreifen glatt durch die Kante (siehe unten links). Zebrastreifen ermöglichen es Ihnen auch, Defekte oder Unvollkommenheiten in der Oberfläche zu erkennen (siehe unten rechts):
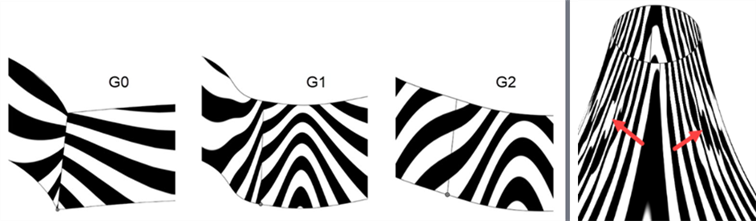
-
Krümmungs-Farbkarte: Ermöglicht eine genauere Untersuchung der Krümmung, indem Sie in einem Part Studio einen Farbverlauf Ihrer Wahl auf eine Fläche oder Oberfläche anwenden. Passen Sie die Skala des Farbverlaufs an und wählen Sie aus verschiedenen Arten von Farbkarten für die beste visuelle Darstellung, um die Kontinuität der Oberfläche und den Übergang zwischen Kanten zu erkennen.
Die gängigste Option für die Krümmung einer Farbkarte ist Gaußsch. Sie ist hilfreich, um festzustellen, ob lokale Unvollkommenheiten oder drastische Änderungen der Oberflächenkrümmung vorliegen. Die im obigen Zebrastreifenbild festgestellte Kräuselung ist bei einer Gaußschen Krümmung deutlicher zu erkennen:

-
V-Stellungs-Analyse: Greifen Sie auf die V-Stellungs-Analysezu, indem Sie in der unteren rechten Ecke der Benutzeroberfläche auf das Symbol „Analyse-Tools anzeigen“ (
 ) klicken. Hier wird der Winkel zwischen den Normalen von zwei Oberflächen an einer gemeinsamen Kante angezeigt. Wenn der Winkel Null ist, sind die beiden Flächen an dieser Stelle entlang der Kante mindestens tangential. Im folgenden Beispiel ändert sich die Rundung bewusst von einer harten Falte zu einer glatten Tangentialverschmelzung am anderen Ende der Kurve:
) klicken. Hier wird der Winkel zwischen den Normalen von zwei Oberflächen an einer gemeinsamen Kante angezeigt. Wenn der Winkel Null ist, sind die beiden Flächen an dieser Stelle entlang der Kante mindestens tangential. Im folgenden Beispiel ändert sich die Rundung bewusst von einer harten Falte zu einer glatten Tangentialverschmelzung am anderen Ende der Kurve: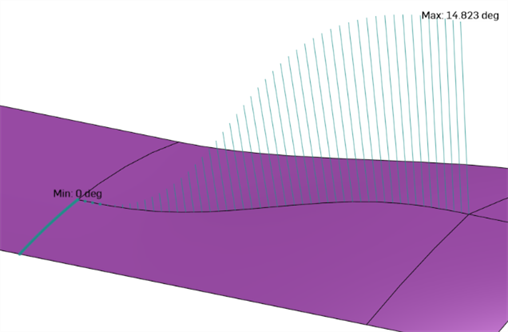
-
Deviation analysis - Display the minimum and maximum deviation between 2 curve chains in a Sketch or Part Studio, or 2 surfaces in a Part Studio.
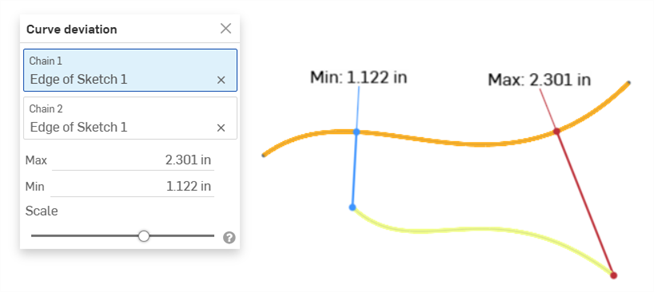
Example showing the Max/Min deviation between two curves
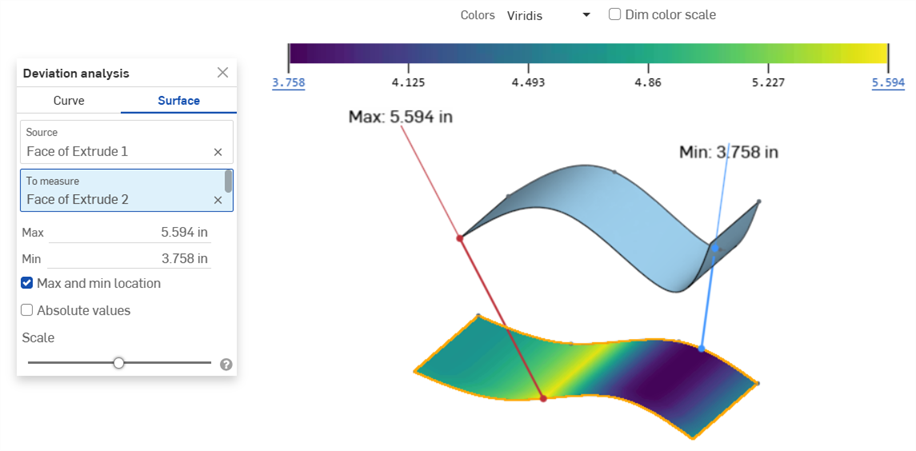
Example showing the Max/Min deviation between a "Source" surface and a surface "To measure"
See Deviation analysis for more information.
-
Reflection analysis - Renders the model in the graphics area with a reflective material and environment image of your preference.

See Reflection analysis for more information.
-
Begrenzungskanten hervorheben: Markieren Sie alle offenen Kanten rot. Wählen Sie dann in der Dropdown-Liste mit den Kamera- und Renderoptionen (
 ) unter dem Ansichtswürfel „Begrenzungskanten hervorheben“ aus. Dies ist nützlich, wenn Sie offene Bereiche in einer Oberfläche identifizieren möchten, die einen Volumenkörper bilden.
) unter dem Ansichtswürfel „Begrenzungskanten hervorheben“ aus. Dies ist nützlich, wenn Sie offene Bereiche in einer Oberfläche identifizieren möchten, die einen Volumenkörper bilden.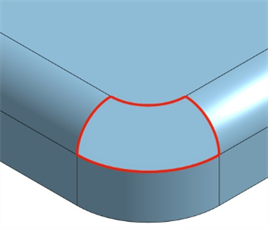
-
Fläche-Tangentenwinkel: Der Tangentenwinkel der Fläche (ein Mess-Tool) liefert eine schnelle Rückmeldung darüber, ob eine Kurve, die sich einer Fläche nähert, an ihrem Endpunkt tangential ist. Wählen Sie die Fläche aus. Der Tangentenwinkel wird links neben dem Mess-Tool angezeigt. Dies ist nützlich, um die Kontinuität vor der Fertigstellung einer Ausformung oder Begrenzungsflächezu testen:
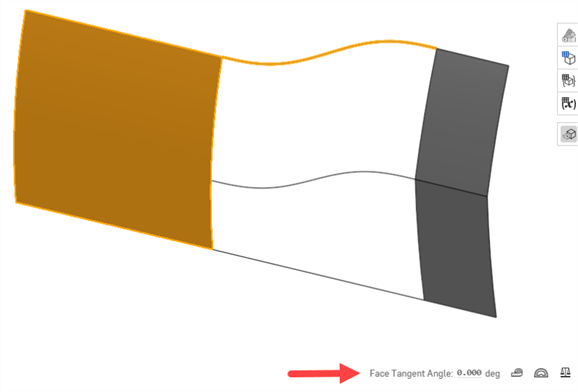
-
In hoher Qualität anzeigen: Aktiviert die Tessellierung mit der höchsten verfügbaren Qualität für die Ansicht und ist unerlässlich, um Kurvenfehler zu erkennen und die Kontinuität genau zu bewerten. Die Anzeige in hoher Qualität finden Sie im Dropdown-Menü für die Kamera- und Renderoptionen (
 ) unter dem Ansichtswürfel.
) unter dem Ansichtswürfel. -
Schattiert mit Kanten/Tangentialkanten: Nützlich, um die Kantenkontinuität klarer zu erkennen. Auf diese beiden Optionen können Sie über das Dropdown-Menü „Kamera“ und „Renderoptionen“ (
 ) unter dem Ansichtswürfel zugreifen.
) unter dem Ansichtswürfel zugreifen.
-
Begrenzungsoberfläche: Einige Features bieten wenig Kontrolle über die Kurven, um eine Oberfläche zu erzeugen, wodurch die Oberflächenqualität übermäßig kompliziert wird und die Oberflächenqualität abnimmt. Eine Begrenzungsoberfläche bietet hier vollständige Kontrolle über die U- und V-Richtungskurven. Die resultierende Oberfläche ist dann nur so kompliziert wie die Eingabekurven. Mit den Features „Ausformung“, „Austragung“ und „Füllung“ werden Kurven in einer oder in beiden Richtungen erzeugt, die nicht kontrolliert werden können, wodurch die Oberfläche komplizierter wird.
Beispielsweise wird dieselbe Oberfläche mit einer Begrenzungsoberfläche und einer Austragung erstellt. Bei der Austragung entstehen Kurven entlang der V-Pfadrichtung, wodurch eine übermäßig komplexe Oberfläche entsteht:
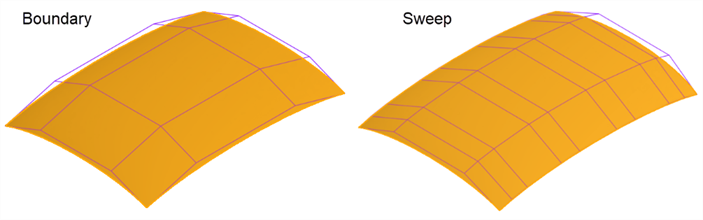
Dieselbe Fläche besteht aus einer Begrenzungsoberfläche und einer Ausformung. Die Ausformung erzeugt ein dichtes Steuerpunkt-Raster in beide Richtungen:
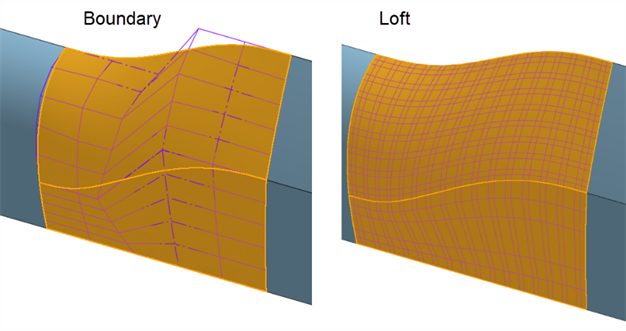
-
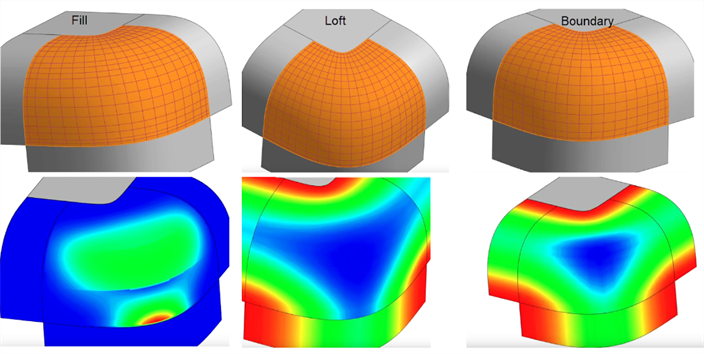
Füllung: Füllen Sie kleine Öffnungen in einer Oberfläche auf. Überprüfen Sie anschließend die resultierende Oberfläche, um eine hochwertige Oberfläche sicherzustellen. Im folgenden Beispiel wird durch Füllen eine nach unten verlaufende Welle hinzugefügt. Die Ausformung erzeugt ein besseres Steuerpunkt-Raster ohne Wellenbildung, aber mit einer Begrenzungsoberfläche erhalten Sie das glatteste und einheitlichste Ergebnis:
-
Flächenüberblendung und Verrundung: Hiermit werden komplexe Kanten erzeugt, die Projektionen oder Teilungsoperationen ähneln. Bei so erzeugten Kanten ist die Wahrscheinlichkeit höher, dass sie nicht gelingen und aufgrund der Komplexität dieser Features zu Unvollkommenheiten führen. Da dies in der Regel kosmetischer Natur ist, ist es am besten, die Oberflächen nach den virtuellen scharfen Kanten aufzubauen und am Ende diese Features hinzuzufügen:

-
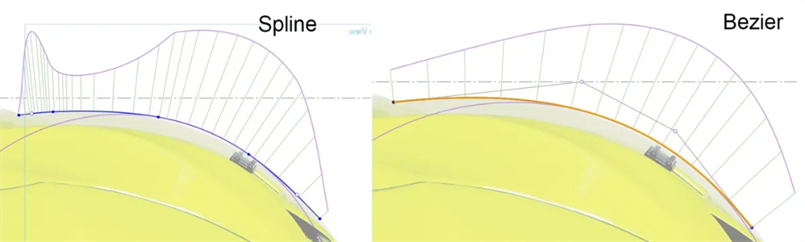
Bézierkurven statt Splines verwenden: Splines haben entlang der Kurve definierte Punkte und Griffe an den Start- und Endpunkten. Bézierkurven haben Steuerpunkte, die entlang des Steuerungspolygons im Abstand zur Kurve definiert sind. Bézierkurven nehmen gleichmäßig zu und ab, ohne dass es zu Unterbrechungen der Kontinuität kommt:
-
Kurven einfach halten: Verwenden Sie das Bézier-Tool und beginnen Sie mit drei oder vier Steuerpunkten (einschließlich Endpunkten). Fügen Sie die geringstmögliche Anzahl an Spline-Punkten hinzu.
-
Der Grad einer Bézierkurve ist die Anzahl der Steuerpunkte minus 1. Bézierkurven sollten im Allgemeinen den Grad 3, 5 oder 7 haben. Es empfiehlt sich, den Grad einer einzelnen Bézierkurve auf 7 zu begrenzen, da die mathematische Berechnung bei höheren Graden sehr komplex wird. Das Verschieben eines Steuerpunkts wirkt sich auf die gesamte Kurve aus. Kurven mit höherem Grad lassen sich nur schwer anpassen, ohne Unvollkommenheiten zu erzeugen.
-
Verwenden Sie einen konsistenten Fluss von Steuerpunkten, um sanfte Krümmungsänderungen ohne unbeabsichtigte Intensitätsänderungen zu gewährleisten.
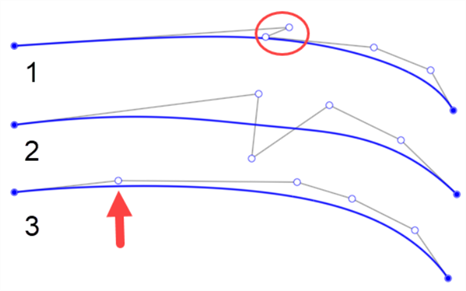
Im Folgenden finden Sie einige Beispiele für Kurven mit schlecht platzierten Steuerpunkten. Der erste Punkt verläuft im Zickzack zwischen dem ersten und dem zweiten Punkt (eingekreist). Der zweite hat Steuerpunkte, die über und unter der Kurve liegen. Es ist nur sinnvoll, die Seite zu ändern, auf der Sie Steuerpunkte platzieren, wenn Sie der Kurve eine Biegung hinzufügen möchten. Bei der dritten Option gibt es keine gleichmäßigen Abstände zwischen den Steuerpunkten. Der Abstand der Punkte zu den anderen Punkten ist stark unterschiedlich (siehe Pfeil unten):
-
-
Nicht von getrimmten Kanten oder projizierten Kurven ausgehen: Da diese durch Trimmvorgänge oder Projektionen mit vielen Spannweiten (zusammengeknoteten Segmenten) von (kubischen) 3-Grad-Splines entstehen, ist alles, was daraus gebaut wird, komplexer und unvollkommener.
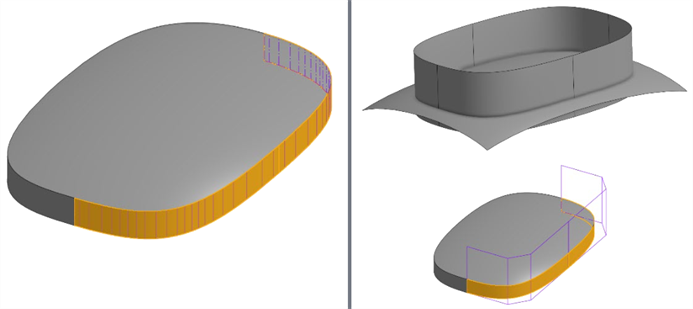
Die Fläche hier hat beispielsweise ein dichteres Steuerpunkt-Raster, wenn eine Regeloberfläche direkt aus der Kante einer getrimmten Fläche (unten links) erstellt wird. Überbauen Sie stattdessen beide Flächen und trimmen Sie die überschüssigen Flächen gemeinsam am Schnittpunkt (unten rechts):
Prüfen Sie, ob anstelle von projizierten Kurven Brückenkurven dieselbe Geometrie mit geringerer Komplexität erstellen können. Brückenkurven sind Bézierkurven, die je nach Endbedingungen bis zu Grad 5 erreichen.
-
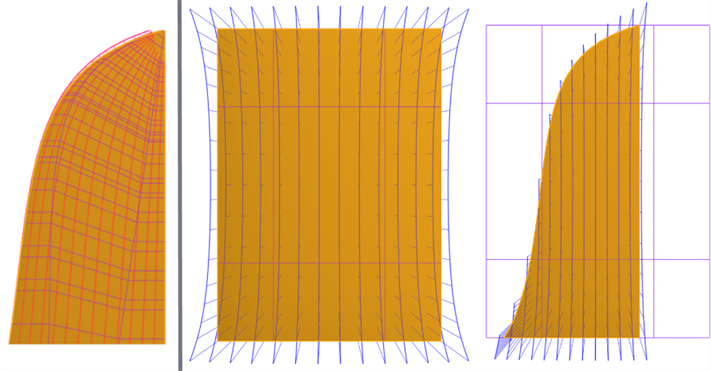
Möglichst vierseitige Oberflächen verwenden: Vierseitige Oberflächen haben das einheitlichste Steuerpunkt-Raster. Das Erstellen einer Oberfläche ohne vier Seiten führt zu Singularitäten (degeneriert) oder zu unregelmäßig angeordneten Steuerpunkten (siehe unten links). Überbauen und trimmen Sie die Oberfläche mithilfe dem Trennen-Feature anhand einer Referenzfläche. Dadurch werden Oberflächen mit unterschiedlichen Kantenprofilen erzeugt, wobei ein einheitliches Steuerpunkt-Raster erhalten bleibt (siehe unten rechts):
-
Möglichst symmetrisch gestalten: Wenden Sie Zwangsbedingungen an, um die Kontinuität und so einen reibungslosen Übergang über die Mittellinie zu gewährleisten.
-
Verwenden Sie Referenzlinien in einer Skizze mit Tangenten- oder Krümmungs-Zwangsbedingungen.
-
Fügen Sie in einem 3D-Modell Referenzflächen hinzu, um die Kontinuität der generierten Oberfläche zu unterstützen.
-
-
Kontextmenüs und Tastaturbefehle verwenden: Arbeiten Sie mit Umschalt+C (Kurven-/Oberflächenanalyse), Umschalt+D (V-Stellungs-Analyse) und Umschalt+R (in hoher Qualität anzeigen). Sie können die Tastaturbefehl-Symbolleiste(n) auch unter „Mein Konto > Einstellungen > Tastenkombinationen > Symbolleisten anpassen“ nach Ihren Vorstellungen konfigurieren.
Hier finden Sie eine unvollständige Liste der Feature-Tools für Oberflächen. Bei der Modellierung von Oberflächenm können weitere Feature-Tools verwendet werden. Siehe Oberflächenbearbeitung.
-
 Verdicken: zum Hinzufügen von Tiefe zu einer Oberfläche hinzu. Erstellen Sie ein neues Bauteil oder bearbeiten Sie ein vorhandenes Bauteil, indem Sie zu einer Oberfläche Wanddicke hinzugeben und sie in einen Volumenkörper umwandeln, Material zu einem vorhandenen Bauteil oder einer Oberfläche hinzufügen bzw. davon entfernen oder Bauteile in ihrem Pfad schneiden.
Verdicken: zum Hinzufügen von Tiefe zu einer Oberfläche hinzu. Erstellen Sie ein neues Bauteil oder bearbeiten Sie ein vorhandenes Bauteil, indem Sie zu einer Oberfläche Wanddicke hinzugeben und sie in einen Volumenkörper umwandeln, Material zu einem vorhandenen Bauteil oder einer Oberfläche hinzufügen bzw. davon entfernen oder Bauteile in ihrem Pfad schneiden. -
 Umschließen:: erstellen Sie ein Bauteil, indem Sie alle Begrenzungen, die einen leeren Raum umgeben, auswählen, um einen Volumenkörper zu bilden. Verwenden Sie alle beliebigen Oberflächen und Volumenkörper (einschließlich Ebenen und Flächen), die sich überschneiden oder sich an einer Begrenzung verbinden, um ein Volumen zu erstellen. Erstellen Sie ein neues Bauteil oder bearbeiten Sie ein vorhandenes Bauteil, indem Sie Bauteile hinzufügen, entfernen oder Bauteile überschneiden.
Umschließen:: erstellen Sie ein Bauteil, indem Sie alle Begrenzungen, die einen leeren Raum umgeben, auswählen, um einen Volumenkörper zu bilden. Verwenden Sie alle beliebigen Oberflächen und Volumenkörper (einschließlich Ebenen und Flächen), die sich überschneiden oder sich an einer Begrenzung verbinden, um ein Volumen zu erstellen. Erstellen Sie ein neues Bauteil oder bearbeiten Sie ein vorhandenes Bauteil, indem Sie Bauteile hinzufügen, entfernen oder Bauteile überschneiden. -
 Verrunden: zum Abrunden von scharfen Innen- und Außenkanten. Definieren Sie diese als standardmäßig konstanten Radius, stilisiert konisch oder variabel, indem Sie „Kantenverrundung“ auswählen. Wenden Sie optional eine Vollrundverrundung an, um eine nahtlose Überblendung einer oder mehrerer Flächen zwischen zwei gegenüberliegenden Seiten zu schaffen.
Verrunden: zum Abrunden von scharfen Innen- und Außenkanten. Definieren Sie diese als standardmäßig konstanten Radius, stilisiert konisch oder variabel, indem Sie „Kantenverrundung“ auswählen. Wenden Sie optional eine Vollrundverrundung an, um eine nahtlose Überblendung einer oder mehrerer Flächen zwischen zwei gegenüberliegenden Seiten zu schaffen. -
 Flächenüberblendung: zum Abrunden von scharfen, verbundenen oder getrennten inneren und äußeren Flächen, um eine nahtlose Überblendung zwischen den Flächen zu erzeugen. Sie können hiermit auch die Überblendung lösen, um neue Flächen zu erzeugen, indem Sie einen Radius oder eine konstante Breite definieren. Definieren Sie außerdem den Überblendungsquerschnitt (rollende Kugel oder ausgetragenes Profil), die Symmetrie, die Steuerung, das Trimmen, die Zwangsbedingungen und die Begrenzungen.
Flächenüberblendung: zum Abrunden von scharfen, verbundenen oder getrennten inneren und äußeren Flächen, um eine nahtlose Überblendung zwischen den Flächen zu erzeugen. Sie können hiermit auch die Überblendung lösen, um neue Flächen zu erzeugen, indem Sie einen Radius oder eine konstante Breite definieren. Definieren Sie außerdem den Überblendungsquerschnitt (rollende Kugel oder ausgetragenes Profil), die Symmetrie, die Steuerung, das Trimmen, die Zwangsbedingungen und die Begrenzungen. -
 Fläche löschen: zum Entfernen von Geometrie aus einem Bauteil. Wählen Sie aus, ob die Flächen in der Umgebung durch Dehnen, bis sie sich schneiden, zusammengeführt werden sollen, ob der Hohlraum mit einer Kappe versehen oder offen gelassen werden soll. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist.
Fläche löschen: zum Entfernen von Geometrie aus einem Bauteil. Wählen Sie aus, ob die Flächen in der Umgebung durch Dehnen, bis sie sich schneiden, zusammengeführt werden sollen, ob der Hohlraum mit einer Kappe versehen oder offen gelassen werden soll. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist. -
 Fläche verschieben: verschiebt, dreht oder versetzt eine oder mehrere ausgewählte Flächen. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist.
Fläche verschieben: verschiebt, dreht oder versetzt eine oder mehrere ausgewählte Flächen. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist. -
 Fläche ersetzen: zum Trimmen einer Fläche oder erweitern einer Fläche zu einer neuen Oberfläche. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist.
Fläche ersetzen: zum Trimmen einer Fläche oder erweitern einer Fläche zu einer neuen Oberfläche. Das Tool „Direktbearbeitung“ ist besonders praktisch, wenn Sie die parametrische Historie des Bauteils nicht vorliegen haben, wie es häufig bei einem importierten Bauteil der Fall ist. -
 Versatz der Oberfläche: zum Erstellen einer neuen Oberfläche, indem Sie eine bestehende Fläche, Oberfläche oder Skizzenregion versetzen. Legen Sie den Versatz auf 0 fest, damit die Kopie nicht versetzt wird.
Versatz der Oberfläche: zum Erstellen einer neuen Oberfläche, indem Sie eine bestehende Fläche, Oberfläche oder Skizzenregion versetzen. Legen Sie den Versatz auf 0 fest, damit die Kopie nicht versetzt wird. -
 Begrenzungsoberfläche: zum Erstellen oder Hinzufügen einer Oberfläche, die durch ihre Begrenzungsprofile spezifiziert ist.
Begrenzungsoberfläche: zum Erstellen oder Hinzufügen einer Oberfläche, die durch ihre Begrenzungsprofile spezifiziert ist. -
 Füllen: zum Erstellen einer Oberfläche (oder eines Bauteils aus Oberflächen), indem Sie Begrenzungen definieren und die Oberfläche durch Begrenzungsbedingungen verfeinern (anstatt die Verwendung von Referenzoberflächen fordern).
Füllen: zum Erstellen einer Oberfläche (oder eines Bauteils aus Oberflächen), indem Sie Begrenzungen definieren und die Oberfläche durch Begrenzungsbedingungen verfeinern (anstatt die Verwendung von Referenzoberflächen fordern). -
 Begrenzung verschieben: Verschieben Sie die Begrenzungskanten einer Oberfläche, um sie zu dehnen oder zu trimmen.
Begrenzung verschieben: Verschieben Sie die Begrenzungskanten einer Oberfläche, um sie zu dehnen oder zu trimmen. -
 Regeloberfläche: zum Erstellen einer neuen oder zusätzlichen Regeloberfläche aus einer vorhandenen Kante oder mehreren Kanten einer Skizzenregion.
Regeloberfläche: zum Erstellen einer neuen oder zusätzlichen Regeloberfläche aus einer vorhandenen Kante oder mehreren Kanten einer Skizzenregion. -
 Gegenseitiges Trimmen: zum Trimmen von zwei benachbarten Oberflächen, indem Sie die Schnittpunkte verlängern, um den Trimmvorgang abzuschließen.
Gegenseitiges Trimmen: zum Trimmen von zwei benachbarten Oberflächen, indem Sie die Schnittpunkte verlängern, um den Trimmvorgang abzuschließen. -
 Beschränkte Oberfläche: Sie können eine Oberfläche aus einer Auswahl von Punkten oder Netzdaten innerhalb einer angegebenen Toleranz erstellen, Abweichungen anzeigen und die Oberfläche für Leistung oder Glattheit optimieren.
Beschränkte Oberfläche: Sie können eine Oberfläche aus einer Auswahl von Punkten oder Netzdaten innerhalb einer angegebenen Toleranz erstellen, Abweichungen anzeigen und die Oberfläche für Leistung oder Glattheit optimieren.
Zusätzlich zu den Tools für die Oberflächenbearbeitung werden Kurven verwendet, um die Grundbausteine von Oberflächen zu erstellen.
Hier finden Sie eine unvollständige Liste der Kurven-Feature-Tools. Bei der Bearbeitung von Kurven können weitere Feature-Tools verwendet werden.
- Skizzen-Tools: Tools in der Skizzen-Symbolleiste – wie „Linie, „Ecken-Rechteck“, „Mittelpunktrechteck“, „Mittelpunktkreis“, „3-Punkt-Kreis“, „Tangentialbogen“, „3-Punkt-Bogen“, „Spline“, „Punkt“ und „Konstruktion“ – dienen zum Erstellen einer Skizze in einem Part Studio.
-
 Helix: Zum Erstellen einer Helix mit einer konischen oder zylindrischen Fläche, einer einzelnen Achse oder Z-Achse einer Verknüpfungsverbindung oder einer runden Kante.
Helix: Zum Erstellen einer Helix mit einer konischen oder zylindrischen Fläche, einer einzelnen Achse oder Z-Achse einer Verknüpfungsverbindung oder einer runden Kante. -
 3D Fit Spline: Zum Erstellen eines 3D-angepassten Spline mit mehreren Scheitelpunkten. Dadurch wird eine Kurve erzeugt, die in der Bauteil-Liste unter „Kurven“ aufgeführt ist.
3D Fit Spline: Zum Erstellen eines 3D-angepassten Spline mit mehreren Scheitelpunkten. Dadurch wird eine Kurve erzeugt, die in der Bauteil-Liste unter „Kurven“ aufgeführt ist. -
 Projizierte Kurve: Zum Erstellen einer Kurve von der Projektion zweier Skizzen (Option „Zwei Skizzen“) oder von der Projektion einer Kurve auf einer Fläche (Option „Kurve zu Fläche“).
Projizierte Kurve: Zum Erstellen einer Kurve von der Projektion zweier Skizzen (Option „Zwei Skizzen“) oder von der Projektion einer Kurve auf einer Fläche (Option „Kurve zu Fläche“). -
 Brückenkurve: Zum Erstellen einer Kurve, die zwei Punkte, Scheitelpunkte oder Verknüpfungsverbindungen verbindet. Die entstehende Kurve wird in der Feature-Liste und der Bauteil-Liste aufgeführt.
Brückenkurve: Zum Erstellen einer Kurve, die zwei Punkte, Scheitelpunkte oder Verknüpfungsverbindungen verbindet. Die entstehende Kurve wird in der Feature-Liste und der Bauteil-Liste aufgeführt. -
 Zusammengesetzte Kurve: Zum Darstellen mehrerer Kanten als eine einzige Kurve. Wählen Sie mehrere aneinander grenzende Kanten, Skizzenelemente oder andere Kurven aus. Wenn nicht-aneinandergrenzende Kanten ausgewählt werden, kann dies dazu führen, dass mehrere Kurven erzeugt werden. Die Auswahlen für die einzelnen Kurven müssen sich am Scheitelpunkt der Kurven treffen. (Kurven sind in unter „Bauteile > Kurvenliste“ aufgeführt.)
Zusammengesetzte Kurve: Zum Darstellen mehrerer Kanten als eine einzige Kurve. Wählen Sie mehrere aneinander grenzende Kanten, Skizzenelemente oder andere Kurven aus. Wenn nicht-aneinandergrenzende Kanten ausgewählt werden, kann dies dazu führen, dass mehrere Kurven erzeugt werden. Die Auswahlen für die einzelnen Kurven müssen sich am Scheitelpunkt der Kurven treffen. (Kurven sind in unter „Bauteile > Kurvenliste“ aufgeführt.) -
 Schnittpunkt-Kurve: Zum Erstellen einer Kurve am Schnittpunkt von mindestens zwei Oberflächen oder Flächen. Die Auswahlen müssen sich überschneiden.
Schnittpunkt-Kurve: Zum Erstellen einer Kurve am Schnittpunkt von mindestens zwei Oberflächen oder Flächen. Die Auswahlen müssen sich überschneiden. -
 Kurve trimmen: Zum Trimmen oder verlängern einer Kurve um einen Abstand oder bis zu einem begrenzenden Objekt.
Kurve trimmen: Zum Trimmen oder verlängern einer Kurve um einen Abstand oder bis zu einem begrenzenden Objekt. -
 Isokline: Zum Erstellen einer Isokline auf einer geneigten Fläche. Eine Isokline verläuft auf einer Fläche an Positionen, an denen die Fläche gegenüber der Referenzdefinition eine bestimmte Neigung aufweist. Die resultierende Isokline wird in der Feature-Liste und der Bauteile-Liste aufgeführt.
Isokline: Zum Erstellen einer Isokline auf einer geneigten Fläche. Eine Isokline verläuft auf einer Fläche an Positionen, an denen die Fläche gegenüber der Referenzdefinition eine bestimmte Neigung aufweist. Die resultierende Isokline wird in der Feature-Liste und der Bauteile-Liste aufgeführt. -
 Versatzkurve: Zum Erstellen und Erweitern und/oder Trennen einer neuen Kurve, indem Sie die Kanten der umgebenden Flächen versetzen.
Versatzkurve: Zum Erstellen und Erweitern und/oder Trennen einer neuen Kurve, indem Sie die Kanten der umgebenden Flächen versetzen. -
 Isoparametrische Kurve: Zum Erstellen von glatten Kurven, die entlang einer Fläche oder Oberfläche in U- oder V-Richtung verlaufen.
Isoparametrische Kurve: Zum Erstellen von glatten Kurven, die entlang einer Fläche oder Oberfläche in U- oder V-Richtung verlaufen. -
 Kurve bearbeiten: Zum Bearbeiten einer vorhandenen Kurve durch Auswählen von Skizzenelementen oder Kurven, um eine vereinfachte Näherung anzuwenden, den Grad zu erhöhen, Kontrollkurven-Scheitelpunkte neu zu positionieren und/oder in eine beliebige 2D-Ebene zu planarisieren.
Kurve bearbeiten: Zum Bearbeiten einer vorhandenen Kurve durch Auswählen von Skizzenelementen oder Kurven, um eine vereinfachte Näherung anzuwenden, den Grad zu erhöhen, Kontrollkurven-Scheitelpunkte neu zu positionieren und/oder in eine beliebige 2D-Ebene zu planarisieren. -
 Routing-Kurve: Erstellen Sie eine Mehrpunktkurve über eine oder mehrere Ebenen im 3D-Raum (geführter Pfad). Dies ist nützlich für die Erstellung von Rohrführungen, Verkabelungen und NURBS-Kurven zur erweiterten Oberflächengestaltung.
Routing-Kurve: Erstellen Sie eine Mehrpunktkurve über eine oder mehrere Ebenen im 3D-Raum (geführter Pfad). Dies ist nützlich für die Erstellung von Rohrführungen, Verkabelungen und NURBS-Kurven zur erweiterten Oberflächengestaltung.
Weitere Ressourcen zum Thema „Oberflächenbehandlung“ finden Sie in unserem Learning Center.