Modelado de superficies
![]()
![]()
![]()
Introducción
Una superficie es una representación de un solo lado del exterior de una pieza que no tiene masa ni espesor.
El modelado de superficies es un enfoque de modelado que permite a los diseñadores crear características geométricas complejas y formas orgánicas que las herramientas de modelado sólido no pueden producir por sí solas. El modelado de superficies se usa para más formas y características de forma libre que el modelado sólido.
Por ejemplo, un cubo sólido se puede dividir en seis caras diferentes. Cada cara representa una superficie que encierra el volumen sólido para formar el cubo. La superposición permite construir cada cara del cubo como una superficie individual. Una vez construidos los seis lados del cubo, se suman las superficies y se crea un volumen cerrado que forma una parte sólida.
La geometría de superficie se utiliza para:
-
Crear una pieza sólida:
-
Con la operación Aumentar espesor, una superficie aumenta su espesor para formar una pieza sólida.
-
Con la operación Encerrar, se crea una pieza sólida formando un volumen cerrado, en el que cada arista delimita 2 caras.
-
-
Cree geometría de construcción (líneas divididas para moldes, fusión y unión de geometrías, soporte de pendientes y rellenos para hacer coincidir la curvatura y la tangencia).
-
Sustituya la cara de una pieza sólida por una geometría más compleja (mediante la operación Reemplazar cara).
La continuidad de curvas y superficies es una medida de la suavidad de la conexión entre 2 curvas o 2 superficies donde se conectan. A medida que las curvas y las superficies se construyen para crear modelos geométricos, la continuidad se vuelve importante para crear la forma orgánica más fluida o continua.
La designación G (o geometría) se usa para determinar la continuidad entre curvas y superficies (G0 a G3). En Onshape, estas designaciones se correlacionan con las opciones de «Combinar» de muchas operaciones de curvas y superficies (por ejemplo, curvas de puente, empalme, mezcla de caras y otras). Estas clasificaciones de continuidad se describen a continuación, junto con sus definiciones:
-
G0 (posición coincidente): la posición coincide entre las 2 curvas/superficies. Ambas curvas/superficies comparten una posición común en la unión.
-
G1 (tangente coincidente): la tangencia coincide entre las 2 curvas/superficies. Ambas curvas/superficies se tocan y comparten un ángulo común que es igual en ambos extremos. Un empalme es un buen ejemplo de este tipo de coincidencia de continuidad.
-
G2 (curvatura coincidente): la curvatura (radio) coincide entre las 2 curvas/superficies. Ambas curvas/superficies se tocan, son tangentes y tienen la misma curvatura en el punto en el que se tocan (ambas tienen radios idénticos).
-
G3 (flujo coincidente): el flujo coincide entre las 2 curvas/superficies. Ambas curvas/superficies se tocan, son tangentes, tienen una curvatura similar y muestran la cantidad de cambio en la curvatura a lo largo de la longitud de la curvatura (flujo).
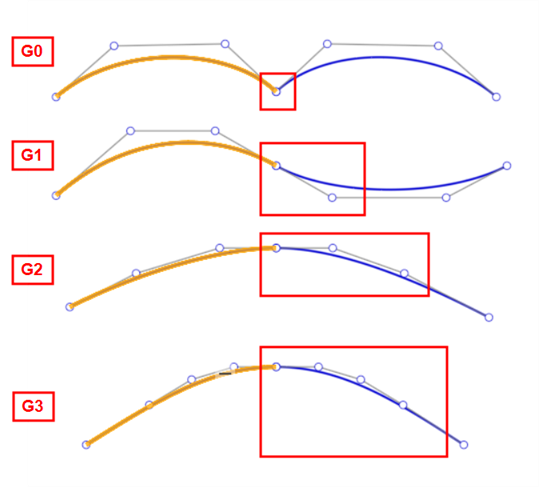
Con la operación Curva coincidente, puede crear una curva coincidente (que se muestra a continuación en naranja) entre dos curvas y hacer coincidir su posición inicial y final, su tangencia, curvatura y flujo (o alguna combinación entre ambas; por ejemplo, hacer coincidir la posición al inicio y hacer coincidir la curvatura al final):
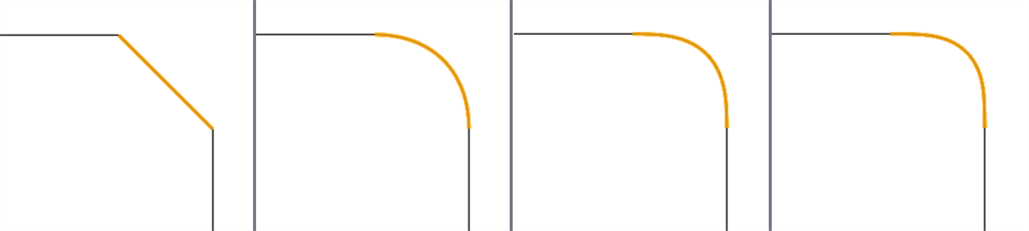
De izquierda a derecha: G0 (posición coincidente), G1 (tangente coincidente), G2 (curvatura coincidente, G3 (flujo coincidente)
Extendiéndolo más allá de las curvas, puede crear una superficie entre dos superficies y hacer coincidir su continuidad inicial y final de la misma manera:

De izquierda a derecha: G0 (posición coincidente), G1 (tangente coincidente), G2 (curvatura coincidente, G3 (flujo coincidente)
Al analizar la continuidad de curvas o superficies con la herramienta de análisis de curvas y superficies, puede observar que con cada coincidencia de continuidad progresiva, las conexiones entre las curvas y superficies se suavizan y muestran peines de curvatura más lisos. G0 (posición coincidente) no se puede analizar mediante el análisis de curva/superficie porque una línea recta no tiene curvatura.
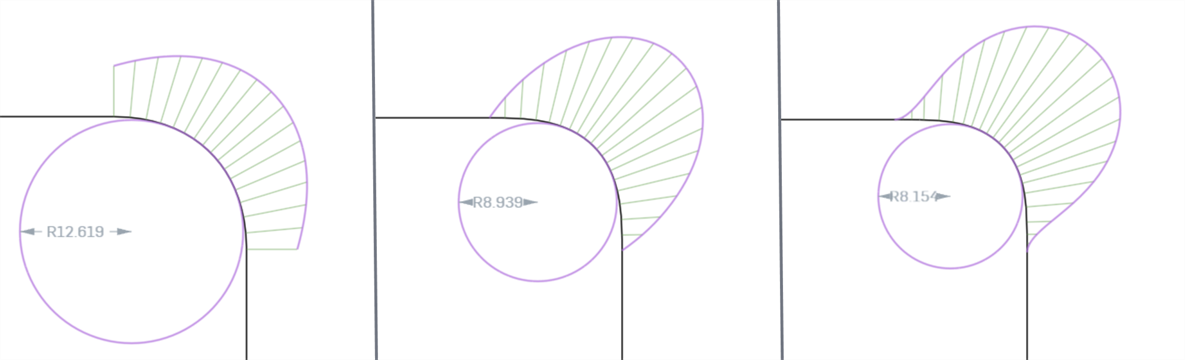
De izquierda a derecha: G1 (tangente coincidente), G2 (curvatura coincidente, G3 (flujo coincidente)
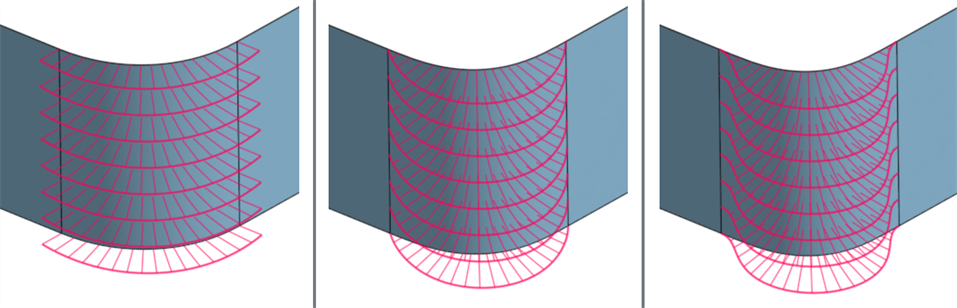
De izquierda a derecha: G1 (tangente coincidente), G2 (curvatura coincidente, G3 (flujo coincidente)
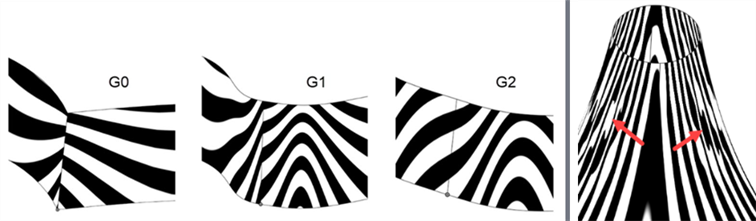
Al analizar la continuidad de curvas o superficies con la herramienta de rayas de cebra, con cada coincidencia de continuidad progresiva, la conexión entre las curvas y superficies se vuelve más suave. Las rayas de cebra en las aristas de la superficie se vuelven cada vez más suaves a medida que se pasa de G0 (posición de coincidencia) a G2 (continuidad de coincidencia):

De izquierda a derecha: G0 (sin continuidad), G1 (tangente coincidente) y G2 (curvatura coincidente)
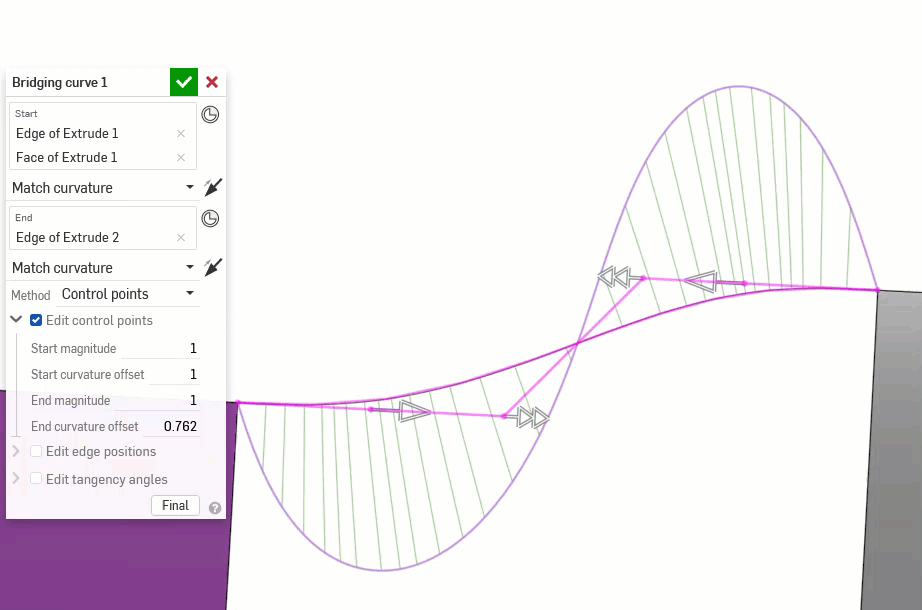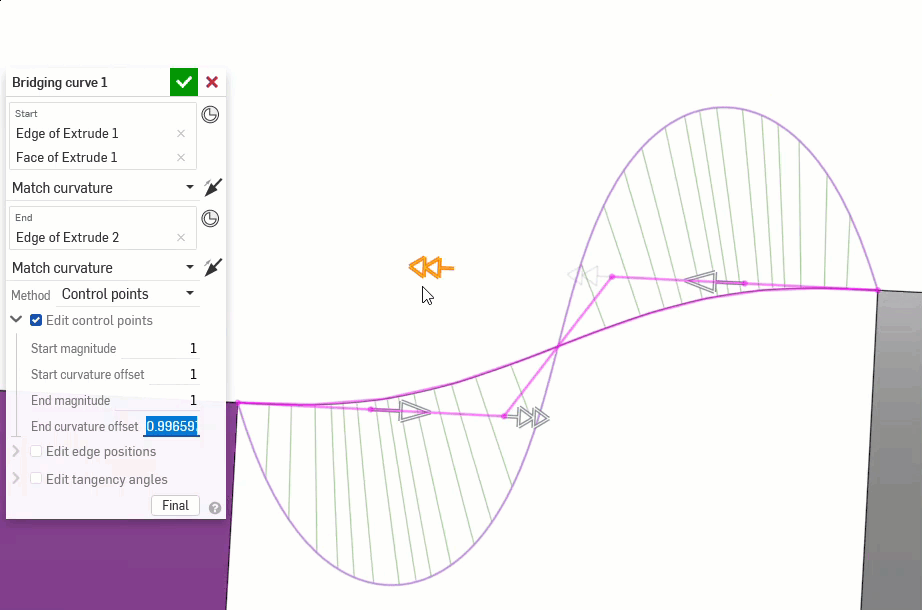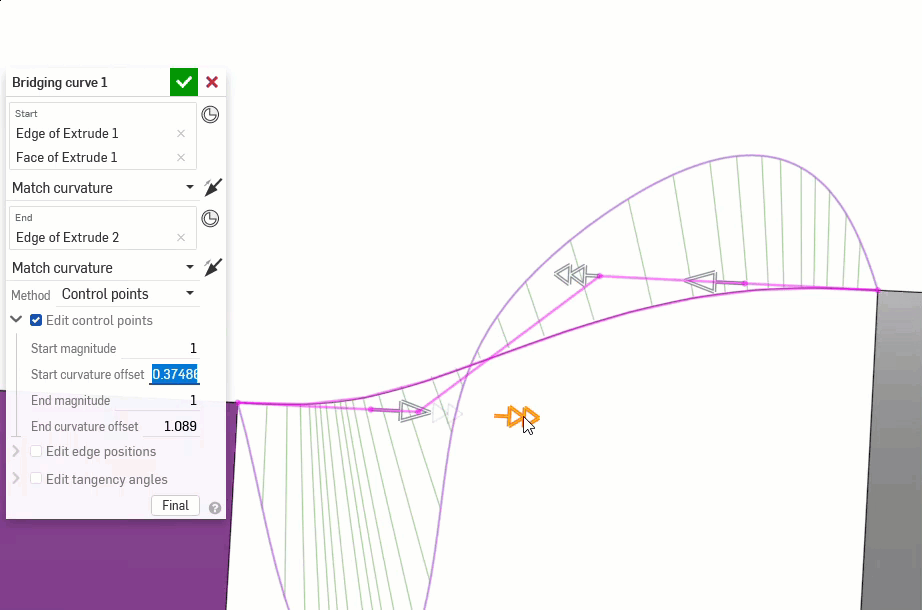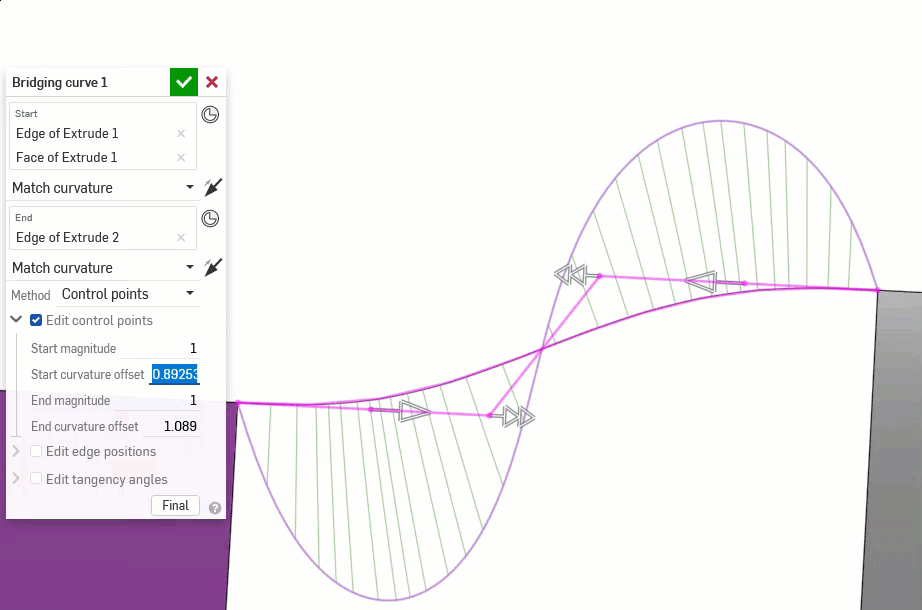
Los siguientes ejemplos ilustran las continuidades en una curva coincidente entre otras dos curvas no lineales. La curva coincidente es de color magenta. La primera columna muestra el diálogo Curva coincidente y la selección de continuidad con el resultado (y la opción Editar puntos de control habilitada), la columna central muestra la curva coincidente con la edición de puntos de control desactivada y la última columna muestra el análisis de curvas/superficie de todas las curvas:
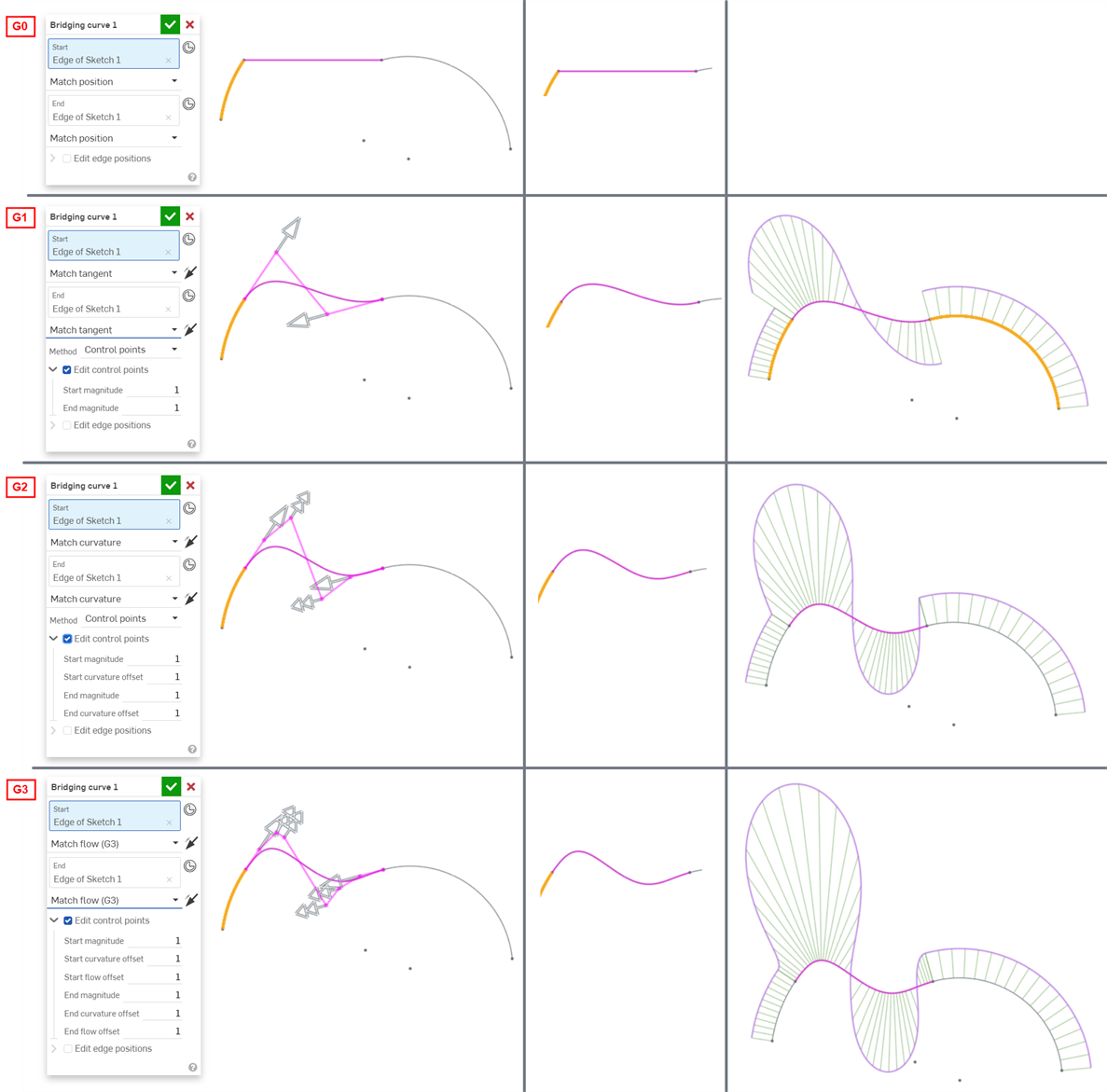
La continuidad seleccionada para las conexiones de curva y superficie del modelo depende completamente del nivel de continuidad requerido en cada unión o arista. No hay una continuidad de superficie correcta o incorrecta.
Además, los órdenes de continuidad más altos requieren más puntos de control para aplicarlos. G0 solo necesita un punto de control (el extremo), G1 necesita dos, G2 necesita tres y G3 necesita cuatro. Una curva de Bézier con restricciones G3 en ambos extremos requiere ocho puntos de control como mínimo, cuatro para cada extremo.
El modelado con superficies requiere pasos adicionales para crear superficies de alta calidad. Estos pasos aumentan el rendimiento, evitan imperfecciones y agilizan la creación de superficies complejas.
-
Análisis de curvas/superficies: visualice y analice la curvatura de un boceto en Part Studio. Para acceder al cuadro de diálogo de análisis de curvas o superficies, pulse Mayús+c, pulse con el botón derecho del mouse en un boceto, una pieza o una superficie, o pulse el icono Mostrar herramientas de análisis (
 ) situado en la esquina inferior derecha de la interfaz.
) situado en la esquina inferior derecha de la interfaz.Estas herramientas muestran los peines de curvatura (la intensidad de la curvatura en un punto determinado a lo largo de una arista o una cara) y las cuadrículas de puntos de control. Lo ideal es que los peines de curvatura aumenten o disminuyan de manera constante.
El siguiente ejemplo se ve bien sin herramientas de evaluación, pero muestra fluctuaciones extremas en la curvatura (especialmente en la dirección U roja, abajo a la izquierda) cuando el análisis de curvatura/superficie está activado. El borde exterior es especialmente problemático (abajo a la derecha):
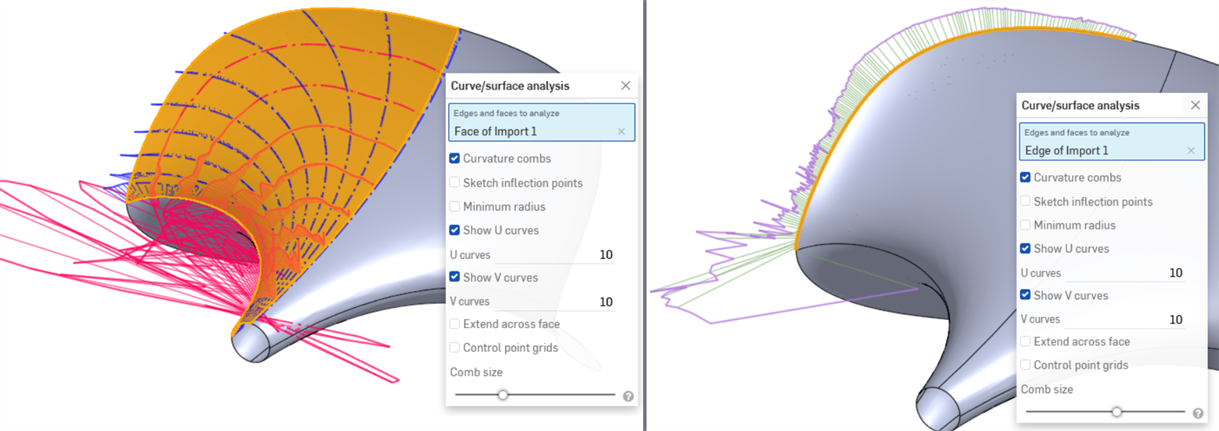
Además, la cuadrícula de puntos de control es una medida de la complejidad de la superficie. El flujo y la densidad de los puntos de control pueden ilustrar un modelo con demasiados puntos de control:

-
Connection analysis - Assess or report the connection between curves and surfaces in a Part Studio or Sketch. Access the Connection analysis dialog from the Show analysis tools icon (
 ) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
-
Mapa de colores y franjas de cebra: las franjas de cebra representan el reflejo de una habitación rayada en el modelo, las caras o las superficies actuales en Part Studio o un Ensamblaje. Esto le permite ver si la curvatura de las aristas y las caras está alineada y es continua o no. Acceda a las franjas de cebra desde el icono Mostrar herramientas de análisis (
 ) en la esquina inferior derecha de la interfaz.
) en la esquina inferior derecha de la interfaz.Las franjas de cebra no coinciden con G0 ni con la continuidad posicional. En la continuidad G1 o tangencial, coinciden directamente en la arista, pero divergen bruscamente. En G2 o continuidad de curvatura, las franjas de cebra atraviesan suavemente la arista (se muestra abajo a la izquierda). Las franjas de cebra también permiten ver defectos o imperfecciones en la superficie (se muestran abajo a la derecha):
-
Mapa de colores de curvatura: permite una investigación más profunda de la curvatura al aplicar un degradado de color de su elección a una cara o superficie en un estudio de piezas. Ajuste la escala del degradado de color y elija entre los distintos tipos de mapas de color para obtener la mejor representación visual que permita distinguir la continuidad de la superficie y la transición entre las aristas.
La opción de curvatura del mapa de colores más común es la gaussiana, que es útil para determinar si hay imperfecciones locales o cambios drásticos en la curvatura de la superficie. La ondulación detectada en la imagen de franjas de cebra de arriba es más evidente si se observa con la curvatura gaussiana:

-
Análisis diédrico: acceda al análisis diédrico seleccionando el icono Mostrar herramientas de análisis (
 ) en la esquina inferior derecha de la interfaz. Muestra el ángulo entre las normales de dos superficies en una arista compartida. Si el ángulo es cero, las dos superficies son al menos tangentes en esa posición a lo largo de la arista. En el ejemplo siguiente, el diedro cambia intencionadamente de un pliegue duro a una mezcla tangente suave en el otro extremo de la curva:
) en la esquina inferior derecha de la interfaz. Muestra el ángulo entre las normales de dos superficies en una arista compartida. Si el ángulo es cero, las dos superficies son al menos tangentes en esa posición a lo largo de la arista. En el ejemplo siguiente, el diedro cambia intencionadamente de un pliegue duro a una mezcla tangente suave en el otro extremo de la curva: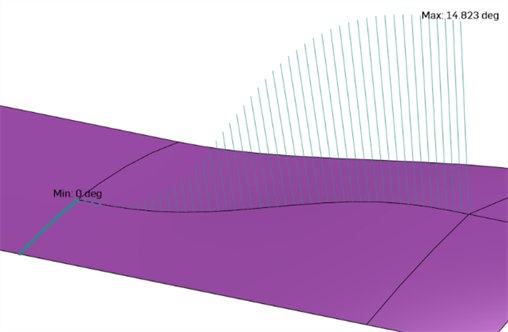
-
Deviation analysis - Display the minimum and maximum deviation between 2 curve chains in a Sketch or Part Studio, or 2 surfaces in a Part Studio.
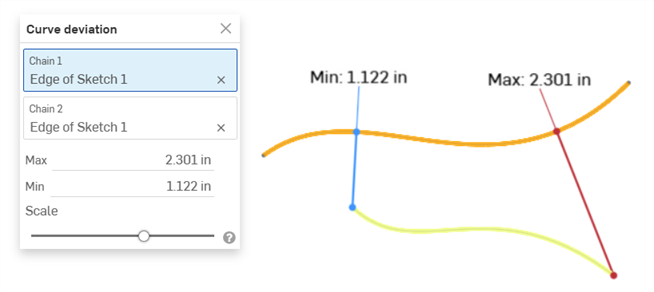
Example showing the Max/Min deviation between two curves
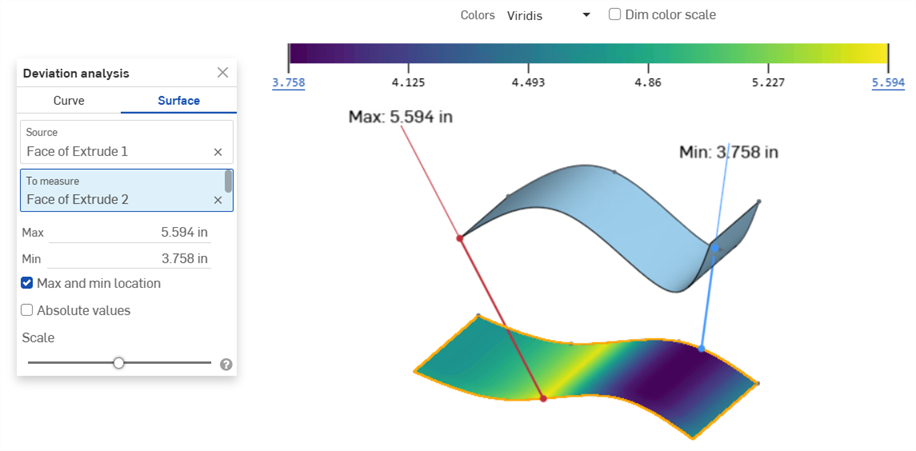
Example showing the Max/Min deviation between a "Source" surface and a surface "To measure"
See Deviation analysis for more information.
-
Reflection analysis - Renders the model in the graphics area with a reflective material and environment image of your preference.

See Reflection analysis for more information.
-
Resaltar las aristas de límite: resalta las aristas abiertas en rojo. Acceda a Resaltar las aristas de límite desde el menú desplegable de opciones de cámara y renderizado (
 ) situado debajo del Cubo de vista. Esto resulta útil cuando se intenta identificar cualquier área abierta en una superficie para formar un sólido.
) situado debajo del Cubo de vista. Esto resulta útil cuando se intenta identificar cualquier área abierta en una superficie para formar un sólido.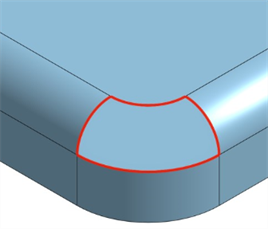
-
Ángulo tangente facial: el ángulo tangente facial (una herramienta de medición) proporciona información rápida sobre si una curva que se acerca a una cara es tangente en su extremo. Seleccione la cara. El ángulo tangente se muestra a la izquierda de la herramienta de medición. Esto resulta útil para comprobar la continuidad antes de completar una solevación o superficie de límite:
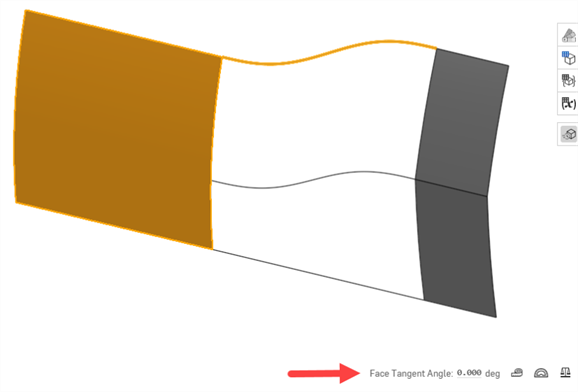
-
Ver en alta calidad: activa la superposición en mosaico de la más alta calidad disponible para la vista y es esencial para identificar las imperfecciones de las curvas y evaluar la continuidad con precisión. Acceda a la vista en alta calidad desde el menú desplegable de opciones de cámara y representar (
 ) situado debajo del Cubo de vista.
) situado debajo del Cubo de vista. -
Sombreado con aristas/aristas tangentes: útil para ver la continuidad de las aristas con mayor claridad. Acceda a ambas opciones desde el menú desplegable de opciones de cámara y renderizado (
 ) situado debajo del Cubo de vista.
) situado debajo del Cubo de vista.
-
Superficie límite: algunas operaciones proporcionan poco control sobre las curvas para crear una superficie, lo que complica demasiado y reduce la calidad de la superficie. Una superficie límite proporciona un control total sobre las curvas en dirección U y V. La superficie resultante es tan complicada como las curvas de entrada. Las operaciones de solevación, barrido y relleno crean curvas en una o ambas direcciones que no se pueden controlar, lo que complica la superficie.
Por ejemplo, la misma superficie se construye con una superficie límite y un barrido. El barrido desarrolla curvas en la dirección en V a lo largo del trazado, creando una superficie demasiado compleja:
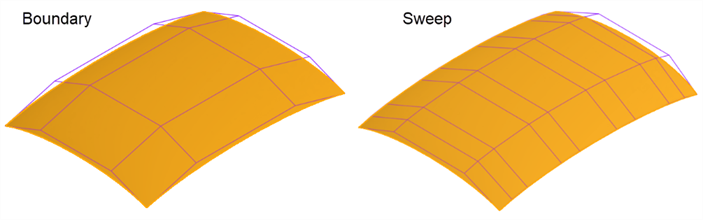
La misma superficie está construida con una superficie límite y una solevación. La solevación crea una densa rejilla de puntos de control en ambas direcciones:
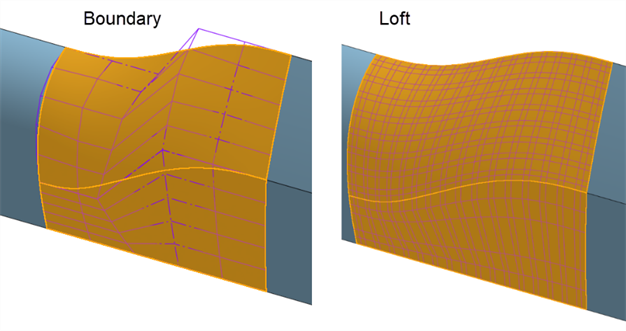
-
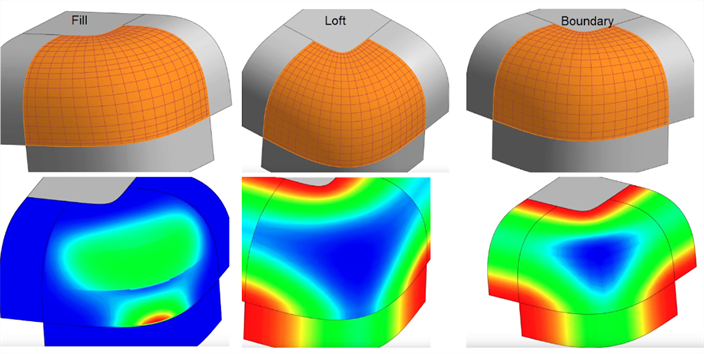
Rellenar: rellena parches pequeños agujeros en una superficie. Después de usar el relleno, evalúe la superficie resultante para garantizar una superficie de calidad. En el ejemplo siguiente, Rellenar añade una ondulación hacia la parte inferior. La solevación crea una mejor rejilla de puntos de control sin ondulaciones, pero la superficie límite crea el resultado más suave y uniforme:
-
Mezcla y redondeo de cara: la mezcla y el redondeo de caras crean aristas complejas similares a las proyecciones o las operaciones de partición. Las aristas creadas con Mezcla y redondeo de caras tienen más probabilidades de fallar e introducir imperfecciones debido a la complejidad de estas operaciones. Como esto suele ser cosmético, lo mejor es construir las superficies a partir de los objetos puntiagudos virtuales y añadir estas características al final:

-
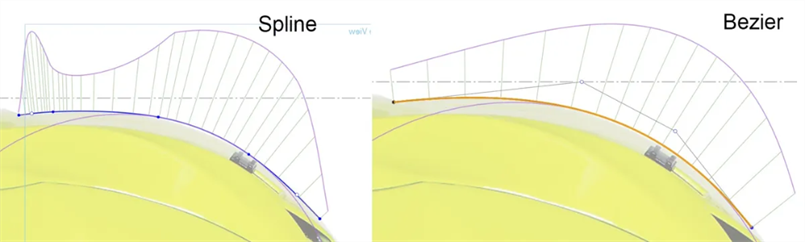
Utilice Béziers en lugar de splines: las splines tienen puntos definidos a lo largo de la curva y puntos de control en los puntos inicial y final. Los Béziers tienen puntos de control definidos a lo largo del polígono de control desplazado con respecto a la curva. Las curvas de Bézier aumentan y disminuyen suavemente sin interrupciones de continuidad:
-
Mantenga las curvas simples: utilice la herramienta Bézier y comience con 3 o 4 puntos de control (incluidos los extremos). Añada la menor cantidad posible de puntos de Spline.
-
El grado de un Bézier es el número de puntos de control menos 1. Por lo general, los Béziers deben ser de grado 3, 5 o 7. Lo mejor es limitar el grado de una sola curva de Bézier a 7 porque el cálculo matemático se vuelve muy complejo en grados más altos. El movimiento de un punto de control afecta a toda la curva, y las curvas de mayor grado son difíciles de ajustar sin introducir imperfecciones.
-
Utilice un flujo uniforme de puntos de control para garantizar cambios de curvatura suaves sin cambios de intensidad no deseados.
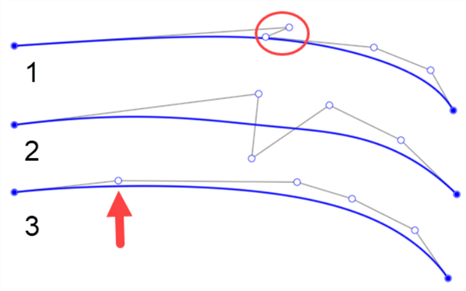
A continuación se muestran algunos ejemplos de curvas con puntos de control mal colocados. La primera tiene un zigzag entre el primer y el segundo punto (delineado por un círculo). El segundo tiene puntos de control situados por encima y por debajo de la curva. Solo es apropiado cambiar el lado en el que se colocan los puntos de control cuando se pretende añadir una inflexión a la curva. El tercero no tiene un espaciado uniforme entre los puntos de control. El espaciado de los puntos en comparación con los demás es drásticamente diferente (se indica con la flecha que aparece a continuación):
-
-
Evite construir a partir de aristas recortadas o curvas proyectadas: dado que se hacen a partir de operaciones de recorte o proyecciones con muchos tramos (segmentos anudados) de estrías de grado 3 (cúbicas), cualquier cosa que se construya a partir de ellas es más compleja e imperfecta.
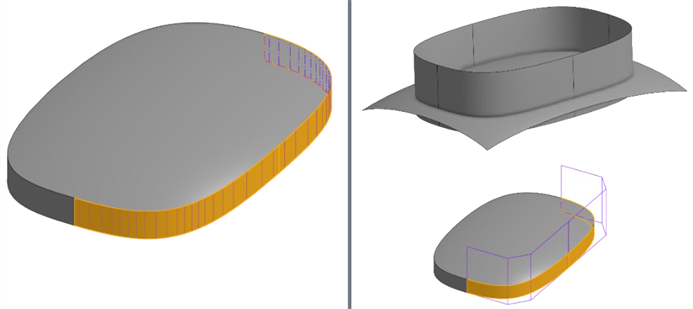
Por ejemplo, la superficie aquí tiene una rejilla de puntos de control más densa cuando se crea una superficie reglada directamente desde el borde de una superficie recortada (abajo a la izquierda). En su lugar, sobreconstruya ambas superficies y utilice un recorte mutuo para recortar el exceso en la intersección (abajo a la derecha):
En lugar de curvas proyectadas, compruebe si las curvas puente pueden crear la misma geometría con menos complejidad. Las curvas puente son curvas de Bézier que alcanzan hasta un grado 5, según las condiciones finales.
-
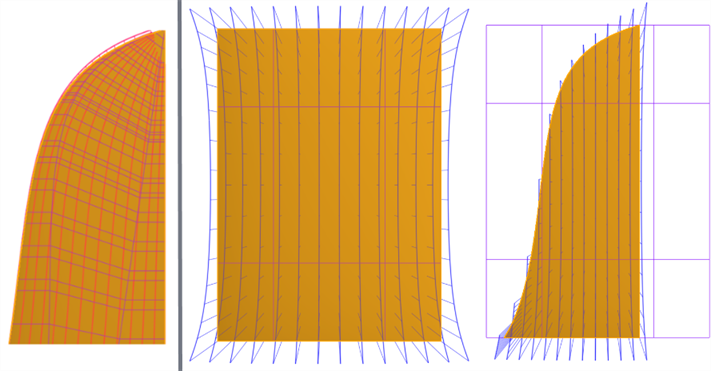
Intente utilizar superficies de cuatro lados: las superficies de cuatro lados tienen la cuadrícula de puntos de control más uniforme. La creación de una superficie sin cuatro lados produce singularidades (degeneran) o puntos de control espaciados irregularmente (se muestran en la parte inferior izquierda). Reconstruya y recorte la superficie con una superficie de referencia mediante la función de división. Esto crea superficies con diferentes perfiles de borde y, al mismo tiempo, mantiene una cuadrícula de puntos de control uniforme (se muestra en la parte inferior derecha):
-
Utilice la simetría cuando sea posible: aplique restricciones de continuidad para garantizar una transición suave a través de la línea central.
-
Utilice líneas de referencia en un boceto con restricciones de tangente o curvatura.
-
En un modelo 3D, añada superficies de referencia para contribuir a la continuidad de la superficie generada.
-
-
Utilice menús contextuales y teclas rápidas: utilice shift+c (análisis de curvas/superficies), shift+d (análisis diédrico) y shift+r (visualización en alta calidad). También puede personalizar el acceso directo de barra de herramientas desde Mi cuenta > Prefrencias > Acceso directo de barra de herramientas.
Aquí se muestra la colección de herramientas de operaciones de superficie. Esta no es una lista exhaustiva. Se pueden utilizar herramientas de operaciones adicionales al modelar superficies. Consulte Creación de superficies para obtener más información.
-
 Espesor: agregue profundidad a una superficie. Cree una pieza nueva o modifique una existente al otorgarle espesor a una superficie y conviértala en un sólido. Para esto, agregue o quite material de una pieza o superficie existentes, o de las piezas que hacen intersección en su trayectoria.
Espesor: agregue profundidad a una superficie. Cree una pieza nueva o modifique una existente al otorgarle espesor a una superficie y conviértala en un sólido. Para esto, agregue o quite material de una pieza o superficie existentes, o de las piezas que hacen intersección en su trayectoria. -
 Encerrar: cree una pieza seleccionando todos los límites que rodean un espacio vacío para formar un sólido. Utilice cualquier conjunto de superficies y sólidos (incluidos planos y caras) que hagan intersección entre sí o se conecten en un límite para crear un volumen. Cree una pieza nueva o modifique una existente agregando, eliminando o haciendo intersecar piezas.
Encerrar: cree una pieza seleccionando todos los límites que rodean un espacio vacío para formar un sólido. Utilice cualquier conjunto de superficies y sólidos (incluidos planos y caras) que hagan intersección entre sí o se conecten en un límite para crear un volumen. Cree una pieza nueva o modifique una existente agregando, eliminando o haciendo intersecar piezas. -
 Redondeo: redondee las aristas interiores y exteriores de intersección y defínalas como un radio constante estándar, una cónica más estilizada o una variable mediante la selección de Redondeo de arista. Si lo desea, aplique un redondeo completo para crear una combinación perfecta de una o más caras entre dos lados opuestos.
Redondeo: redondee las aristas interiores y exteriores de intersección y defínalas como un radio constante estándar, una cónica más estilizada o una variable mediante la selección de Redondeo de arista. Si lo desea, aplique un redondeo completo para crear una combinación perfecta de una o más caras entre dos lados opuestos. -
 Pliegue de cara: redondee las caras interiores y exteriores puntiagudas, conectadas o desconectadas, para crear un pliegue perfecto entre las caras o separe el pliegue para crear nuevas caras mediante la definición de un radio o un ancho constante. Defina en mayor detalle la sección transversal del pliegue (bola rodante o perfil de barrido), la simetría, el control, el recorte, las restricciones y los límites.
Pliegue de cara: redondee las caras interiores y exteriores puntiagudas, conectadas o desconectadas, para crear un pliegue perfecto entre las caras o separe el pliegue para crear nuevas caras mediante la definición de un radio o un ancho constante. Defina en mayor detalle la sección transversal del pliegue (bola rodante o perfil de barrido), la simetría, el control, el recorte, las restricciones y los límites. -
 Eliminar cara: elimine la geometría de una pieza. Seleccione si desea reparar las caras circundantes (extendiéndolas hasta que se intersequen), cubrir el vacío o dejarlo abierto. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada.
Eliminar cara: elimine la geometría de una pieza. Seleccione si desea reparar las caras circundantes (extendiéndolas hasta que se intersequen), cubrir el vacío o dejarlo abierto. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada. -
 Mover cara: desplace, gire o desfase una o más caras seleccionadas. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada.
Mover cara: desplace, gire o desfase una o más caras seleccionadas. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada. -
 Reemplazar cara: recorte una cara o alargue una cara a una superficie nueva. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada.
Reemplazar cara: recorte una cara o alargue una cara a una superficie nueva. Esta herramienta de edición directa es especialmente práctica si no tiene el historial paramétrico de la pieza, como suele ocurrir con una pieza importada. -
 Desfasar superficie: se crea una nueva superficie mediante el desfase de una región de boceto, superficie o cara existente. Establezca la distancia de desfase en 0 para crear una copia en su lugar.
Desfasar superficie: se crea una nueva superficie mediante el desfase de una región de boceto, superficie o cara existente. Establezca la distancia de desfase en 0 para crear una copia en su lugar. -
 Superficie límite: cree o añada una superficie especificada por sus perfiles límite.
Superficie límite: cree o añada una superficie especificada por sus perfiles límite. -
 Rellenar: cree una superficie (o una pieza a partir de superficies) definiendo límites y refinando la superficie con condiciones de límite (en lugar de requerir el uso de superficies de referencia).
Rellenar: cree una superficie (o una pieza a partir de superficies) definiendo límites y refinando la superficie con condiciones de límite (en lugar de requerir el uso de superficies de referencia). -
 Mover límite: mueva las aristas de los límites de una superficie para alargarla o recortarla.
Mover límite: mueva las aristas de los límites de una superficie para alargarla o recortarla. -
 Superficie reglada: cree una superficie reglada nueva o adicional a partir de una arista existente o de varias aristas de una región de boceto.
Superficie reglada: cree una superficie reglada nueva o adicional a partir de una arista existente o de varias aristas de una región de boceto. -
 Recorte mutuo: recorte dos superficies adyacentes extendiendo las intersecciones para completar el recorte.
Recorte mutuo: recorte dos superficies adyacentes extendiendo las intersecciones para completar el recorte. -
 Superficie restringida: crea una superficie a partir de una selección de puntos o datos de malla dentro de una tolerancia especificada. Muestra las desviaciones y optimiza el rendimiento o la suavidad.
Superficie restringida: crea una superficie a partir de una selección de puntos o datos de malla dentro de una tolerancia especificada. Muestra las desviaciones y optimiza el rendimiento o la suavidad.
Además de las herramientas de superficie, las curvas se utilizan para crear los componentes básicos de las superficies.
Aquí se muestra la colección de herramientas de operaciones de curvas. Esta no es una lista exhaustiva. Se pueden utilizar herramientas de operaciones adicionales al manipular curvas.
- Herramientas de boceto: las herramientas de la barra de herramientas de boceto, como línea, rectángulo por esquina, rectángulo por punto central, círculo de punto central, círculo por 3 puntos, arco tangente, arco por 3 puntos, punto de spline y construcción, se utilizan para crear un boceto en un Part Studio.
-
 Hélice: cree una hélice con una cara cónica o cilíndrica, un eje único o un eje Z de un conector de relación o una arista circular.
Hélice: cree una hélice con una cara cónica o cilíndrica, un eje único o un eje Z de un conector de relación o una arista circular. -
 Ajuste a spline 3D : cree un ajuste a spline 3D a través de una serie de vértices. Crea una curva que aparece en la lista de piezas en Curvas.
Ajuste a spline 3D : cree un ajuste a spline 3D a través de una serie de vértices. Crea una curva que aparece en la lista de piezas en Curvas. -
 Curva proyectada: cree una curva a partir de la proyección de dos bocetos (opción Dos bocetos) o de la proyección de una curva en una cara (opción Curva a cara).
Curva proyectada: cree una curva a partir de la proyección de dos bocetos (opción Dos bocetos) o de la proyección de una curva en una cara (opción Curva a cara). -
 Curva puente: cree una curva que conecte dos puntos, vértices o conectores de relación. La curva resultante aparece en la lista de operaciones y en la lista de piezas.
Curva puente: cree una curva que conecte dos puntos, vértices o conectores de relación. La curva resultante aparece en la lista de operaciones y en la lista de piezas. -
 Curva compuesta: representa varios bordes como una sola curva. Seleccione varias aristas, entidades de croquis y otras curvas adyacentes. La selección de aristas no contiguas puede provocar la creación de varias curvas. Las selecciones para cada curva deben coincidir en sus vértices. (Las curvas aparecen en la lista Piezas > Curvas).
Curva compuesta: representa varios bordes como una sola curva. Seleccione varias aristas, entidades de croquis y otras curvas adyacentes. La selección de aristas no contiguas puede provocar la creación de varias curvas. Las selecciones para cada curva deben coincidir en sus vértices. (Las curvas aparecen en la lista Piezas > Curvas). -
 Curva de intersección: cree una curva en la intersección de dos o más superficies o caras. Las selecciones deben hacer intersección.
Curva de intersección: cree una curva en la intersección de dos o más superficies o caras. Las selecciones deben hacer intersección. -
 Recortar curva: recorta o alarga una curva una distancia o hasta una entidad delimitadora.
Recortar curva: recorta o alarga una curva una distancia o hasta una entidad delimitadora. -
 Isoclina: crea una isoclina en una cara inclinada. Una isoclina recorre una cara en posiciones en las que la cara tiene una pendiente determinada en comparación con su definición de referencia. La isoclina resultante aparece en la lista de operaciones y en la lista de piezas.
Isoclina: crea una isoclina en una cara inclinada. Una isoclina recorre una cara en posiciones en las que la cara tiene una pendiente determinada en comparación con su definición de referencia. La isoclina resultante aparece en la lista de operaciones y en la lista de piezas. -
 Curva de desfase: cree y alargue o divida una nueva curva desplazando las aristas de las caras circundantes.
Curva de desfase: cree y alargue o divida una nueva curva desplazando las aristas de las caras circundantes. -
 Curva isoparamétrica: cree curvas suaves que discurran a lo largo de una cara o superficie en la dirección U o V.
Curva isoparamétrica: cree curvas suaves que discurran a lo largo de una cara o superficie en la dirección U o V. -
 Editar curva: edite una curva existente seleccionando entidades de boceto o curvas para aplicar una aproximación simplificada, elevar el grado, reposicionar los vértices de la curva de control o planarizar en cualquier plano 2D.
Editar curva: edite una curva existente seleccionando entidades de boceto o curvas para aplicar una aproximación simplificada, elevar el grado, reposicionar los vértices de la curva de control o planarizar en cualquier plano 2D. -
 Curva de enrutamiento: crea una curva con varios puntos en uno o más planos del espacio 3D (trayectoria enrutada). Esto es útil para crear curvas de enrutamiento de tuberías, cableado y NURBS para superficies avanzadas.
Curva de enrutamiento: crea una curva con varios puntos en uno o más planos del espacio 3D (trayectoria enrutada). Esto es útil para crear curvas de enrutamiento de tuberías, cableado y NURBS para superficies avanzadas.
Para obtener más recursos sobre superficies, visite nuestro Centro de aprendizaje.