Introduction

A surface is a single sided representation of a part's exterior that does not have a mass or thickness.

Surface modeling is a modeling approach that allows designers to create complex geometric features and organic shapes that solid modeling tools cannot produce alone. Surface modeling is used for more free-form shapes and features than solid modeling.

For example, a solid cube can be broken out into six different faces. Each face represents a surface that encloses the solid volume to form the cube. Surfacing lets you build each face of the cube as an individual surface. After all six sides of the cube are built, the surfaces are added together, and an enclosed volume is created, forming a solid part.

Surface geometry is used to:

  • Create a solid part:

    • Using the Thicken feature, a surface is thickened to form a solid part.

    • Using the Enclose feature, a solid part is created by forming a closed volume, where every edge bounds 2 faces.

  • Create construction geometry (split lines for molds, blending and bridging geometry together, supporting lofts and fills for matching curvature and tangency).

  • Replace a solid part face with more complex geometry (using the Replace face feature).

Curve and surface continuity is a measure of the smoothness of the between 2 curves or 2 surfaces where they connect. As curves and surfaces are built up to create geometric models, continuity becomes important in order to create the most fluid or continuous organic shape.

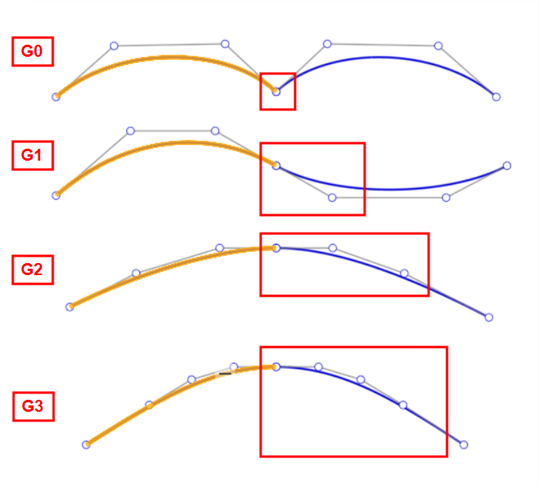
The G (or Geometry) designation is used to determine curve/surface continuity (G0 to G3). In Onshape, these designations correlate to the "Match" options in many curve and surface features (for example, Bridging curves, Fillet, Face blend, and others). These continuity classifications are outlined below, along with their definitions:

  • G0 (Match position) - The position is matched between the 2 curves/surfaces. Both curves/surfaces share a common position at the joint.

  • G1 (Match tangent) - Tangency is matched between the 2 curves/surfaces. Both curves/surfaces touch and share a common angle that is equal at both ends. A fillet is a good example of this type of continuity match.

  • G2 (Match curvature) - Curvature (radius) is matched between the 2 curves/surfaces. Both curves/surfaces touch, are tangent, and have the same curvature at the point where they touch (they both have identical radii).

  • G3 (Match flow) - Flow is matched between the 2 curves/surfaces. Both curves/surfaces touch, are tangent, have similar curvature, and show the amount of change in the curvature over the curvature's length (flow).

Using the Bridging curve feature, you can create a bridging curve (shown below in orange) between two curves and match its start and end position, tangency, curvature, and flow (or some combination between the two; for instance, Match position at the start and Match curvature at the end):

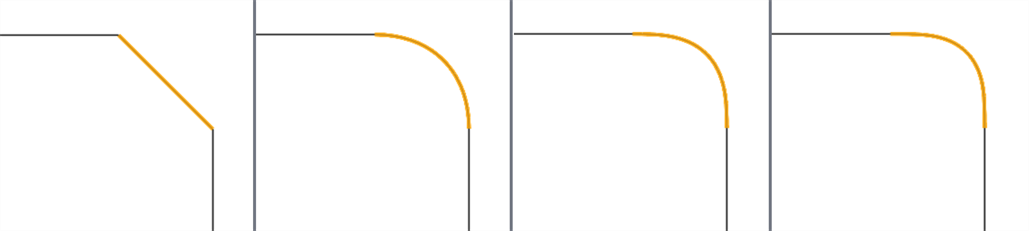
Curve continuities

From left to right: G0 (Match position), G1 (Match tangent), G2 (Match curvature), G3 (Match flow)

Extending this beyond curves, you can create a surface between 2 surfaces, and match its start and end continuity in the same way:

Surface continuities

From left to right: G0 (Match position), G1 (Match tangent), G2 (Match curvature), G3 (Match flow)

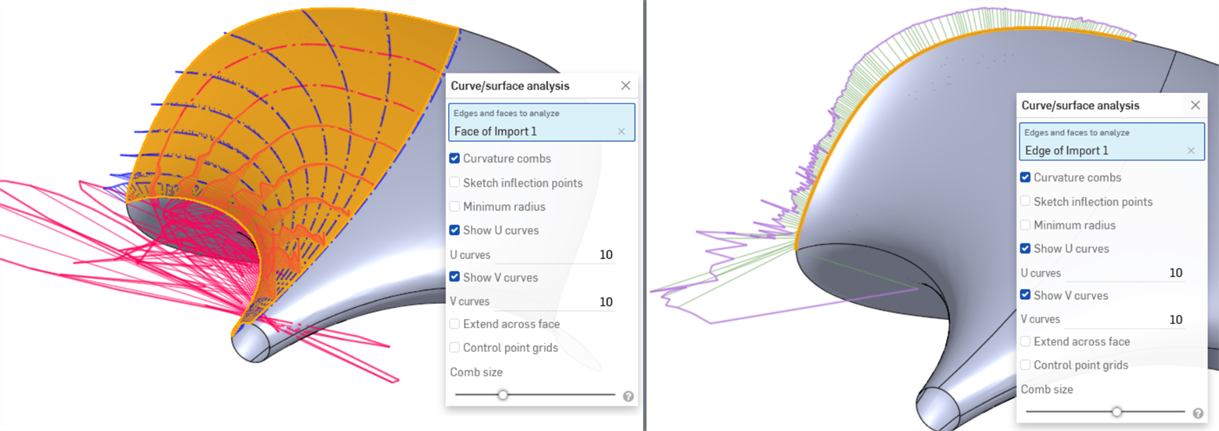
When analyzing curve or surface continuity using the Curve/surface analysis tool, you can see that with each progressive continuity match, the connections between the curves/surfaces becomes smoother and show smoother curvature combs. G0 (Match position) cannot be analyzed using the Curve/surface analysis because a straight line has no curvature.

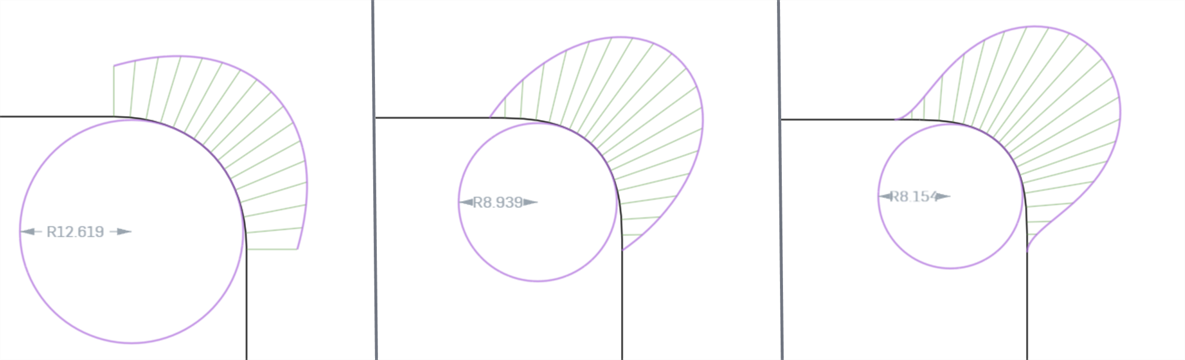
Curve/surface analysis of continuities

From left to right: G1 (Match tangent), G2 (Match curvature), G3 (Match flow)

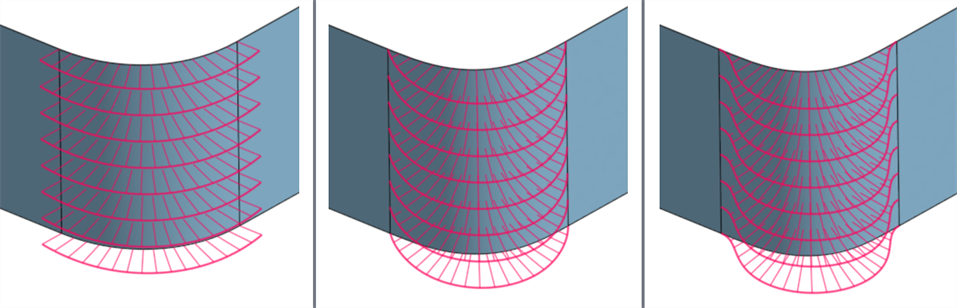
Analyzing surface continuity

From left to right: G1 (Match tangent), G2 (Match curvature), G3 (Match flow)

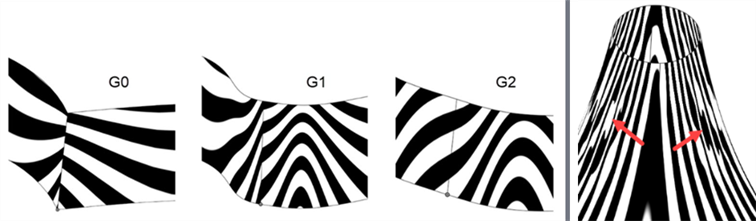
When analyzing curve or surface continuity using the Zebra stripes tool, with each progressive continuity match, the connection between the curves/surfaces becomes smoother. Zebra stripes at the surface edges become increasingly smooth as you go up from G0 (Match position) to G2 (Match continuity):

Zebra stripes used to analyze continuity

From left to right: G0 (No continuity), G1 (Match tangent), and G2 (Match curvature)

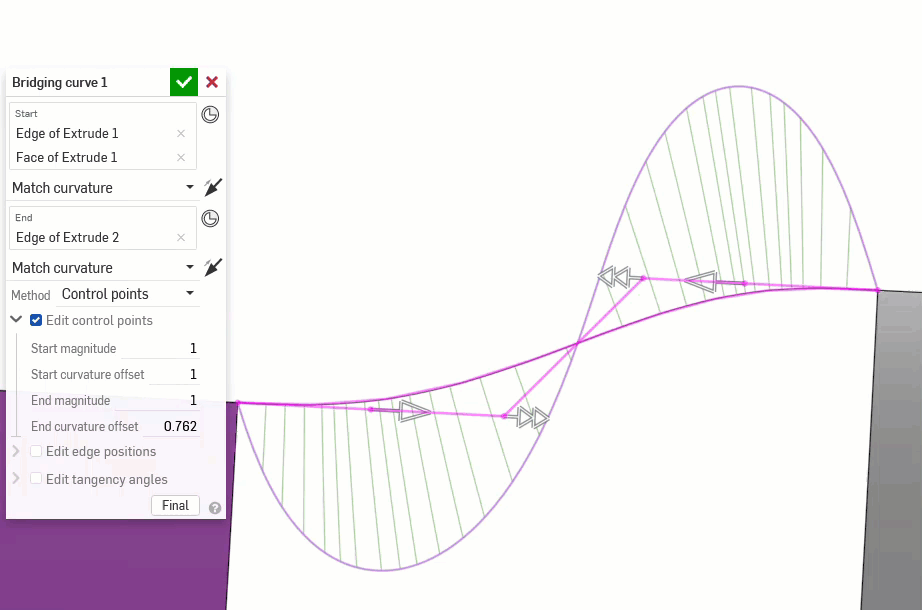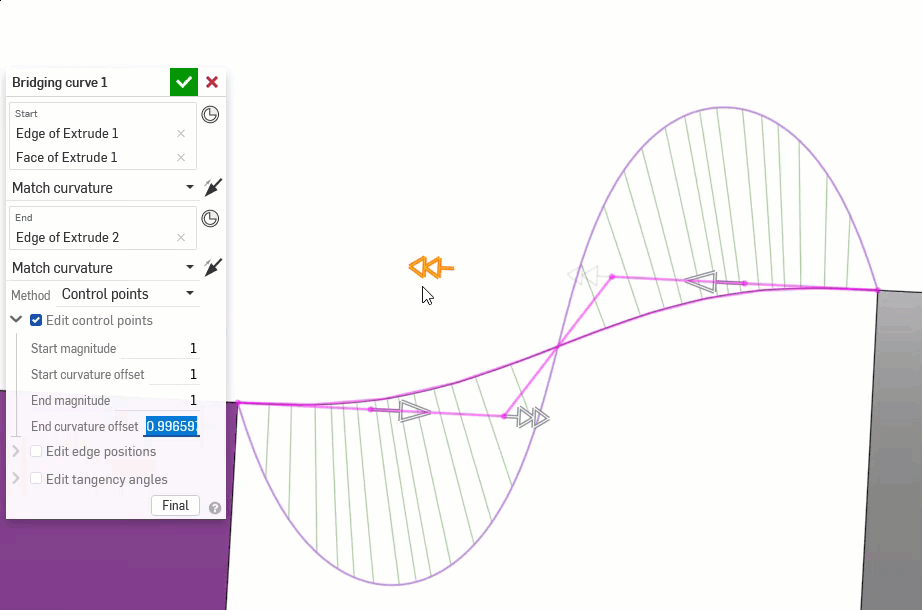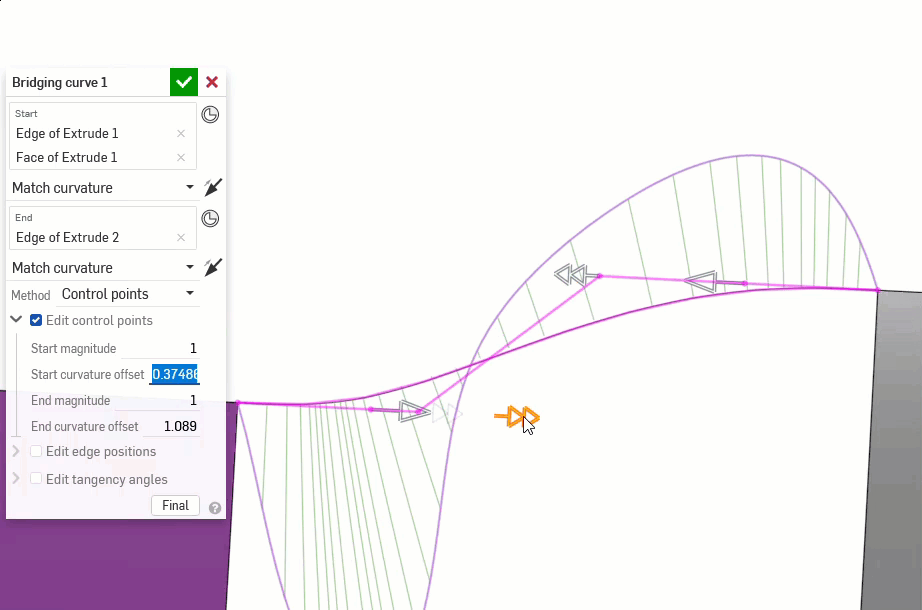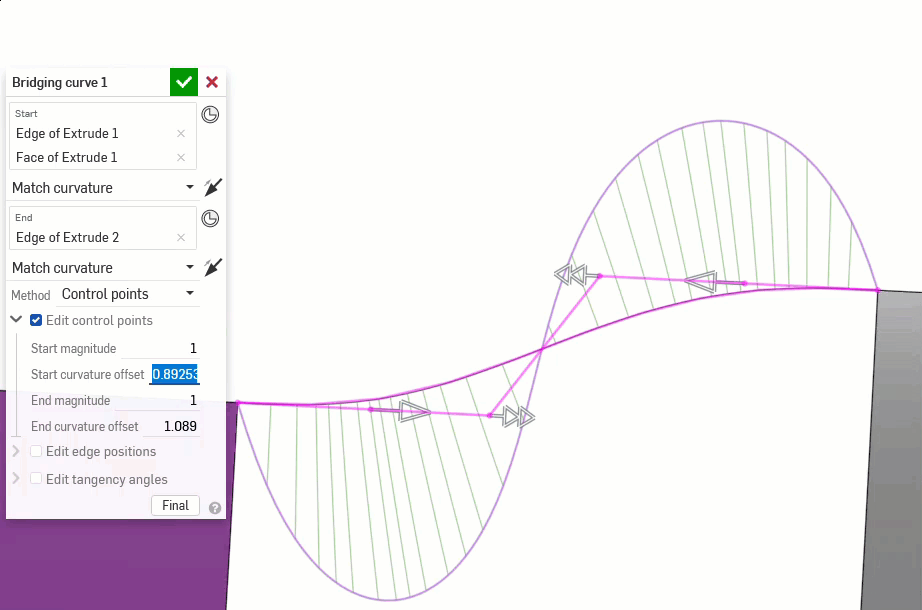
The following examples illustrate the continuities on a bridging curve between two other non-linear curves. The bridging curve is colored magenta. The first column shows the Bridging curve dialog and continuity selection with the result (and Edit control points enabled), the middle column shows the bridging curve with Edit control points disabled, and the final column shows the Curve/surface analysis for all curves:

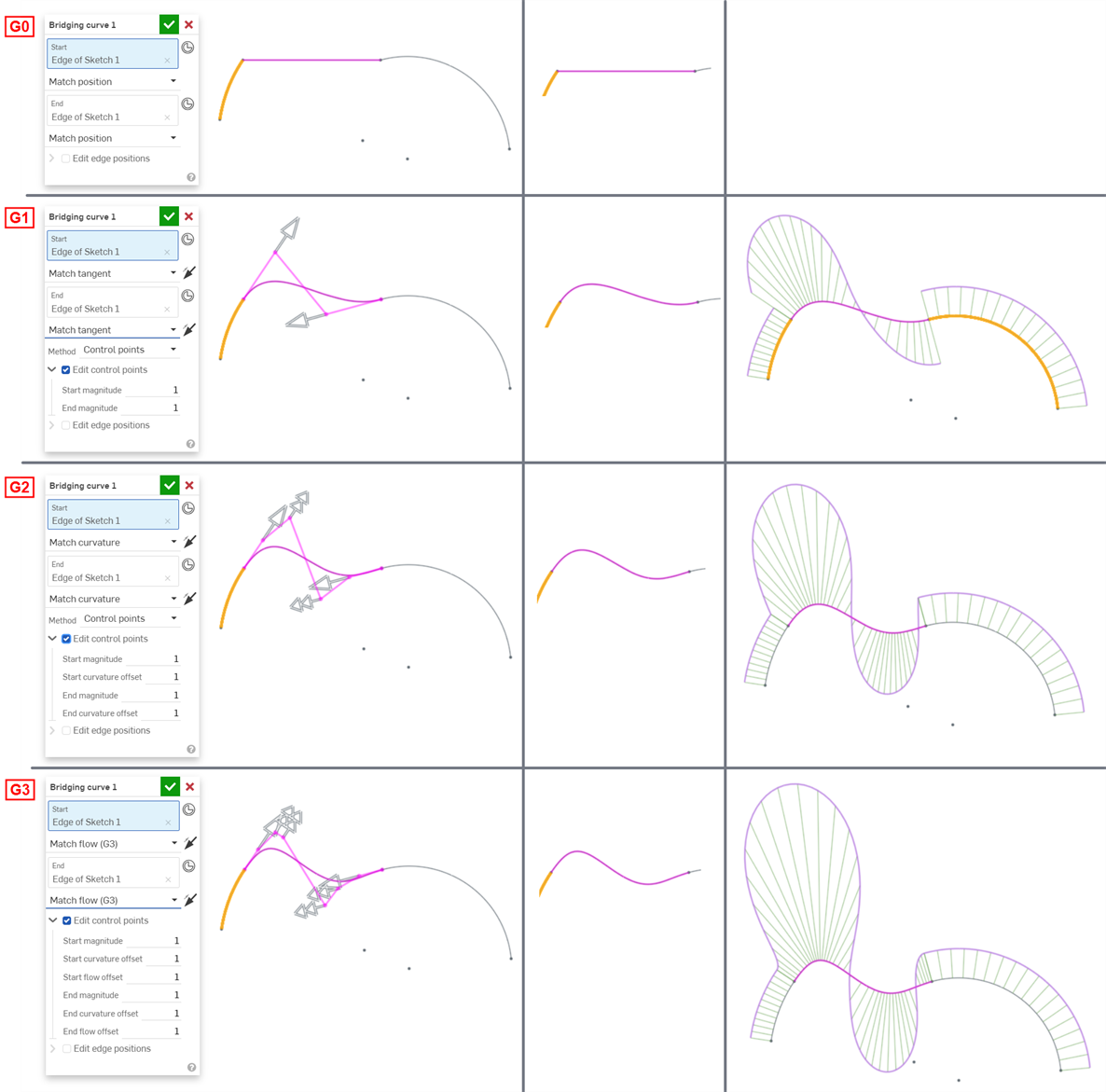
Continuity examples on a bridging curve between 2 non-linear curves

The continuity selected for the curve and surface connections in your model depends entirely on the level of continuity required at each junction/edge. There is no right or wrong surface continuity.

Additionally, higher orders of continuity require more control points to enforce. G0 needs only one control point (the endpoint), G1 needs two, G2 needs three, and G3 needs four. A Bezier curve that is G3 constrained at both ends requires at least eight control points, four for each end.

Control values (control points) and continuity

Modeling with surfaces requires additional steps to create high quality surfaces, These steps increase performance, avoid imperfections, and streamline complex surface creation.

  • Curve/surface analysis - Visualize and analyze curvature on a sketch in the Part Studio. Access the Curve/surface analysis dialog by clicking Shift+c, right-clicking on a sketch, part, or surface, or clicking the Show analysis tools icon () at the interface's bottom right corner.

    These tools show curvature combs (the intensity of the curvature at a certain point along an edge or face), and control point grids. Ideally, the curvature combs should have steady increases or decreases.

    The following example looks good without evaluation tools but shows extreme fluctuations in curvature (especially in the red U direction below left) when Curvature/surface analysis is enabled. The outer edge is especially problematic (below right):

    Curve analysis examples

    Additionally, the control point grid is a measure of the complexity of the surface. The flow and density of control points can illustrate a model with too many control points: 

    Curve analysis dense Control point grid example

  • Zebra stripes and Color map - Zebra stripes represent the reflection of a striped room on the current model, faces, or surfaces in a Part Studio or Assembly. This allows you to see whether or not the curvature across edges and faces are aligned and continuous. Access Zebra stripes from the Show analysis tools icon () at the bottom right corner of the interface.

    Zebra stripes do not match up with G0 or positional continuity. In G1 or tangency continuity, they match up directly on the edge but diverge sharply. In G2 or curvature continuity, the zebra stripes pass smoothly through the edge (shown below left). Zebra stripes also allow you to see defects or imperfections in the surface (shown below right):

    Zebra stripe examples

  • Curvature color map - Enables deeper investigation of curvature by applying a gradient of color of your choosing onto a face or surface in a Part Studio. Adjust the scale of the color gradient and choose from different types of color maps to gain the best visual representation to discern surface continuity and transition between edges.

    The most common color map curvature option is Gaussian, which is helpful in determining if there are local imperfections or drastic changes in surface curvature. The rippling detected in the above Zebra stripes image is more apparent viewed with Gaussian curvature:

    Curvature Color map with Gaussian curvature

  • Dihedral analysis - Access Dihedral analysis by selecting the Show Analysis tools icon () at the bottom right corner of the interface. This displays the angle between the normals of 2 surfaces at a shared edge. If the angle is zero, the 2 surfaces are at least tangent at that location along the edge. In the example below, the dihedral intentionally changes from a hard crease to a smooth tangent blend at the other end of the curve:

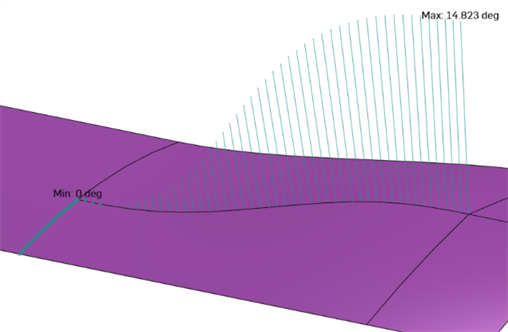
    Dihedral analysis example

  • Highlight boundary edges - Highlight any open edges in red. Access Highlight boundary edges from the Camera and render options dropdown () below the View cube. This is useful when you are trying to identify any open areas in a surface to form a solid.

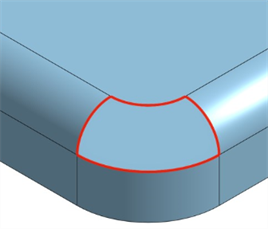
    Highlight boundary edges example

  • Face Tangent Angle - Face Tangent Angle (a Measure tool) provides quick feedback on whether a curve approaching a face is tangent at its endpoint. Select the face. The tangency angle is displayed to the left of the measure tool. This is useful to test continuity before completing a Loft or Boundary surface:

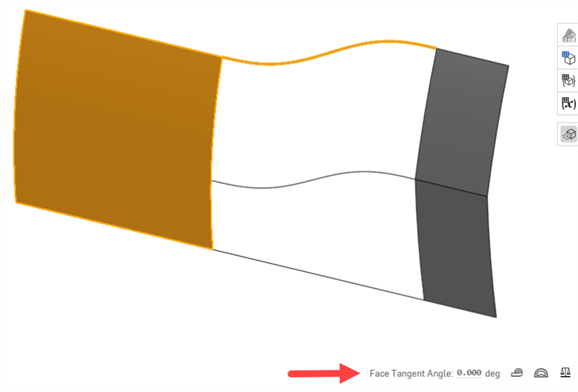
    Face tangent angle example

  • View in high quality - Turns on the highest available quality tessellation for the view and is essential to identify curve imperfections and evaluate continuity accurately. Access View in high quality from the Camera and render options dropdown () below the View cube.

  • Shaded with edges/Tangent edges - Useful to view edge continuity more clearly. Access both these options from the Camera and render options dropdown () below the View cube.

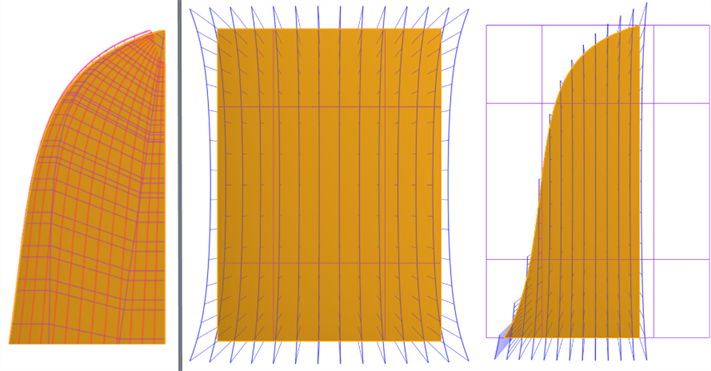
  • Boundary surface - Some features provide little control over the curves to create a surface, over-complicating and decreasing surface quality. A Boundary surface provides complete control over the U and V direction curves. The resultant surface is only as complicated as the input curves. Loft, Sweep, and Fill features create curves in one or both directions that cannot be controlled, complicating the surface.

    For example, the same surface is built with a Boundary surface and a Sweep. The sweep develops curves along the V direction along the path, creating an overly complex surface:

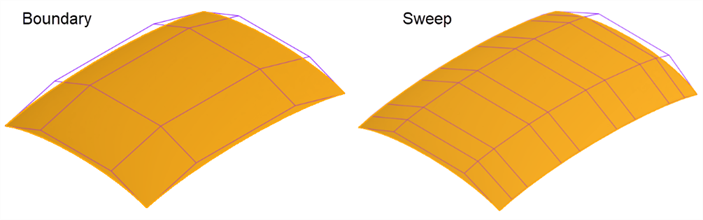
    Boundary surface and sweep example

    The same surface is built with a Boundary surface and a Loft. The Loft creates a dense control point grid in both directions:

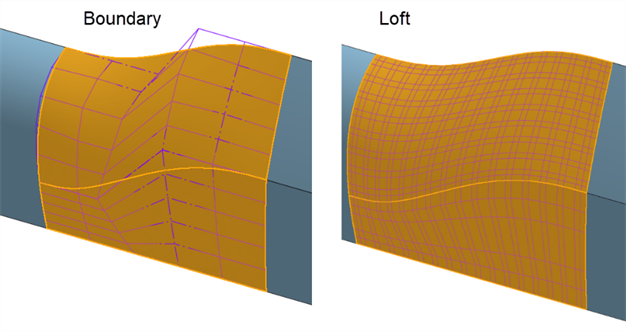
    Boundary surface and loft example

  • Fill - Fill patches small holes in a surface. After using Fill, evaluate the resultant surface to ensure a quality surface. In the example below, Fill adds a ripple towards the bottom. Loft creates a better control point grid with no rippling, but the Boundary surface creates the smoothest, most consistent result:

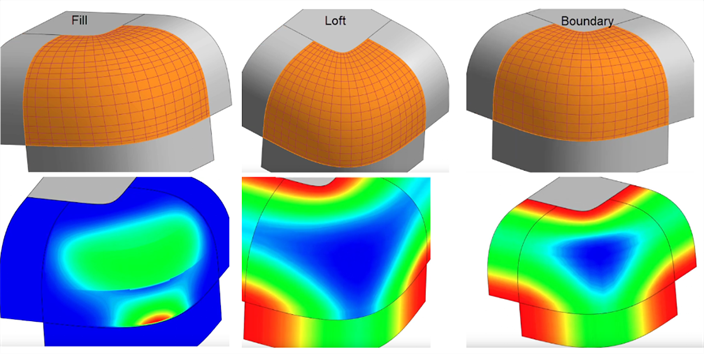
    Fill examples

  • Face Blend and Fillet - Face blend and Fillet create complex edges similar to projections or split operations. Edges created by Face blend or Fillet have a higher chance of failing and introducing imperfections due to the complexity of these features. Since this is usually cosmetic, building the surfaces to the virtual sharps and adding these features at the end is best:

    Face blends and Fillets example

  • Use Beziers instead of Splines - Splines have points defined along the curve and handles on the start and end points. Beziers have control points defined along the control polygon offset from the curve. Bezier curves increases and decreases smoothly with no continuity breaks:

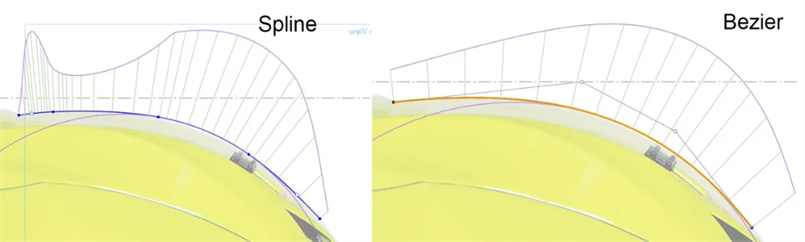
    Spline versus Bezier feature example

  • Keep curves simple - Use the Bezier tool and start with 3 or 4 control points (including endpoints). Add the least possible amount of Spline points.

    • The degree of a Bezier is the number of control points minus 1. Beziers should generally be of the degree 3, 5, or 7. Limiting the degree of a single Bezier curve to 7 is best because the mathematical computation becomes very complex at higher degrees. Moving one control point affects the entire curve, and higher-degree curves are difficult to adjust without introducing imperfections.

    • Use a consistent flow of control points to ensure smooth curvature changes with no unintended intensity changes.

      Below are a few examples of curves with poorly placed control points. The first has a zig-zag between the first and second points (outlined by the circle). The second has control points positioned above and below the curve. It is only appropriate to change which side you place control points on when you intend to add inflection to the curve. The third does not have smooth spacing between control points. The point’s spacing compared with the others is drastically different (indicated by the arrow below):

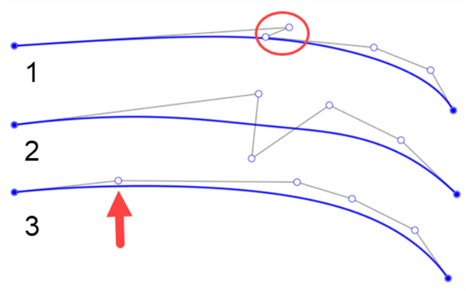
      Besier control point examples

  • Avoid building from trimmed edges or projected curves - Since these are made from trimming operations or projections with many spans (segments knotted together) of degree-3 (cubic) splines, anything built from them is more complex and imperfect.

    For example, the surface here has a denser control point grid when creating a ruled surface directly from a trimmed surface's edge (below left). Instead, overbuild both surfaces and use a Mutual trim to trim the excess at the intersection (below right):

    Trimmed edge example

    Instead of projected curves, see if Bridging curves can build the same geometry with less complexity. Bridging curves are Bezier curves that reach up to degree-5, depending on end conditions.

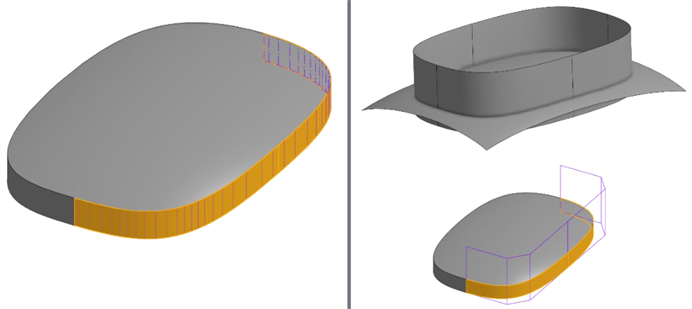
  • Aim to use four-sided surfaces - Four-sided surfaces have the most consistent control point grid. Creating a surface without four sides leads to singularities (degenerates) or irregularly spaced control points (shown below left). Overbuild and trim the surface with a reference surface using the Split feature. This creates surfaces with different edge profiles, while maintaining a consistent control point grid (shown below right):

    Control point consistency example

  • Use symmetry when possible - Apply constraints for continuity to ensure a smooth transition across the centerline.

    • Use reference lines in a sketch with Tangent or Curvature constraints.

    • In a 3D model, add reference surfaces to assist with the continuity of the generated surface.

  • Use shortcut menus and hotkeys - Use shift+c (Curve/surface analysis), shift+d (Dihedral analysis), and shift+r (View in high quality). You can also customize the Shortcut toolbar (s) under My account > Preferences > Shortcut toolbars.

This lists the collection of surface feature tools. This is not an exhaustive list. Additional Feature tools may be used when modeling surfaces. See Surfacing for additional information.

  • Thicken - Add depth to a surface. Create a new part or modify an existing one by giving thickness to a surface and converting it to a solid, adding or removing material from an existing part or surface, or intersecting parts in its path.
  • Enclose - Create a part by selecting all boundaries surrounding an empty space to form a solid. Use any set of surfaces and solids (including planes and faces) that intersect each other or connect at a boundary to create a volume. Create a new part or modify an existing one by adding, removing, or intersecting parts.
  • Fillet - Round sharp interior and exterior edges and define as a standard constant radius, more stylized conic, or variable by selecting Edge fillet. Optionally apply a Full round fillet to create a seamless blend of one or more faces between two opposing sides.
  • Face blend iconFace blend - Round sharp connected or disconnected interior and exterior faces to create a seamless blend between the faces or detach the blend to create new faces, defining a radius or constant width. Further define the blend cross section (rolling ball or swept profile), symmetry, control, trim, constraints, and limits.
  • Delete face - Remove geometry from a part. Select whether to heal the surrounding faces (by extending until they intersect), cap the void, or leave the void open. This Direct Editing tool is especially convenient if you don't have the parametric history of the part, as is often the case with an imported part.
  • Move face - Translate, rotate, or offset one or more selected faces. This Direct Editing tool is especially convenient if you don't have the parametric history of the part, as is often the case with an imported part.
  • Replace face - Trim a face or extend a face to a new surface. This Direct Editing tool is especially convenient if you don't have the parametric history of the part, as is often the case with an imported part.
  • Offset surface - Create a new surface by offsetting an existing face, surface, or sketch region. Set offset distance to 0 to create a copy in place.
  • Loft feature icon Boundary surface - Create or add a surface specified by its boundary profiles.
  • Fill - Create a surface (or a part from surfaces) by defining boundaries and refine the surface with boundary conditions (instead of requiring the use of reference surfaces).
  • Move boundary - Move boundary edges of a surface in order to extend or trim it.
  • Ruled surface - Create a new or additional ruled surface from an existing edge or multiple edges of a sketch region.
  • Mutual trim - Trim two adjacent surfaces by extending intersections to complete the trim.

In addition to the surfacing tools, curves are used to create the basic building blocks of surfaces.

This lists the collection of curve feature tools. This is not an exhaustive list. Additional Feature tools may be used when manipulating curves.

  • Sketch tools - Tools in the Sketch toolbar such as Line, Corner rectangle, Center point rectangle, Center point circle, 3 point circle, Tangent arc, 3 point arc, Spline, Point, and Construction used to create a sketch in a Part Studio.
  • Helix - Create a helix using a conical or cylindrical face, single axis or z-axis of a mate connector, or circular edge.
  • 3D fit spline - Create a 3D fit spline through a series of vertices. Creates a curve which is listed in the Parts list under Curves.
  • Projected curve - Create a curve from the projection of two sketches (Two sketches option) or from the projection of a curve on a face (Curve to face option).
  • Bridging curve - Create a Curve connecting any two points, vertices, or Mate connectors. The resulting Curve is listed in the Feature list and the Parts list.
  • Composite curve - Represent multiple edges as one Curve. Select multiple adjacent edges, sketch entities, and other curves. Selecting non-contiguous edges may result in multiple Curves created. Selections for each Curve must meet at their vertices. (Curves are listed in the Parts > Curves list.)
  • Intersection curve - Create a curve at the intersection of two or more surfaces or faces. The selections must intersect.
  • Trim curve - Trim or extend a curve by a distance or to a bounding entity.
  • Isocline - Create an isocline on a sloped face. An isocline runs on a face at positions where the face has a certain slope compared to its reference definition. The resulting isocline is listed in the Feature list and Parts list.
  • Offset curve - Create and extend and/or split a new curve by offsetting edges on surrounding faces.
  • Isoparametric curve - Create smooth curves that run along a face or surface in the U or V direction.
  • Edit curve - Edit an existing curve by selecting sketch entities or curves to apply a simplified approximation, elevate the degree, reposition control curve vertices and/or planarize into any 2D plane.

For more surfacing resources, visit our Learning center.