简介

曲面是零件外部的单侧表示，没有质量或厚度。

曲面建模是一种建模方法，它允许设计师创建实体建模工具无法单独生成的复杂几何特征和有机形状。与实体建模相比，曲面建模用于更多自由形状和特征。

例如，一个实心立方体可以分成六个不同的面。每个面代表包围立体体积的曲面，形成立方体。曲面允许您将立方体的每个面构建为单独的曲面。在立方体的所有六个面都建好之后，将曲面相拼形成一个封闭的体积，形成一个实体零件。

曲面几何图元用于：

  • 创建实体零件：

    • 使用“加厚”特征，将曲面加厚以形成实体零件。

    • 使用“封闭”特征，通过形成封闭体积来创建实体零件，其中每条边包围 2 个面。

  • 创建构造几何图元（模具的分割线，将几何体混合和桥接在一起，支撑放样和填充以匹配曲率和切线）。

  • 用更复杂的几何图元替换实体零件面（使用“替换面”特征）。

曲线和曲面连续性是衡量两条曲线之间或两个曲面之间相连的平滑度的度量。由于曲线和曲面是为了创建几何模型而构建的，连续性对于创建最流畅或最连续的有机形状变得很重要。

G（或几何图元）名称用于确定曲线/曲面的连续性（G0 到 G3）。在 Onshape 中，这些名称与许多曲线和曲面特征（例如，桥接曲线、圆角、面混合等）中的“匹配”选项相关。这些连续性分类及其定义概述如下：

  • G0（匹配位置） - 该位置在 2 条曲线/曲面之间相匹配。两个曲线/曲面在接头处共享一个共同的位置。

  • G1（匹配切线） - 两条曲线/曲面之间的切线相匹配。两个曲线/曲面接触并共享一个两端相等的共同角度。圆角是这种连续性匹配的一个很好的例子。

  • G2（匹配曲率）- 曲率（半径）在 2 条曲线/曲面之间相匹配。两条曲线/曲面都接触、相切，并且在它们接触的地方具有相同的曲率（它们都有相同的半径）。

  • G3（匹配流动） - 两条曲线/曲面之间的流量相匹配。两条曲线/曲面都接触、相切，具有相似的曲率，并显示曲率在曲率长度（流动）上的变化量。

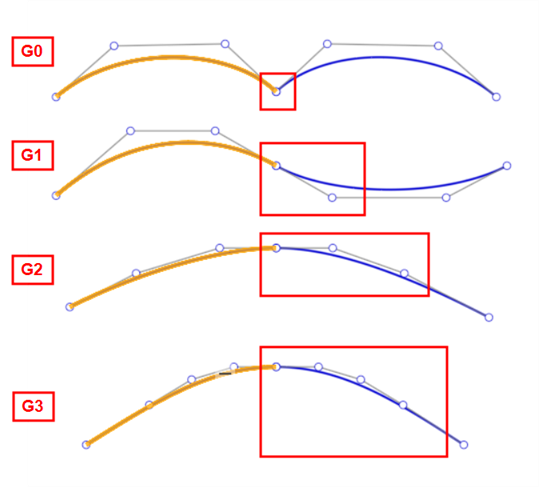
使用桥接曲线特征，可以在两条曲线之间创建桥接曲线（如下橙色所示），并匹配其起点和终点位置、切线、曲率和流动（或两者之间的某种组合；例如，在起点匹配位置并在末端匹配曲率）：

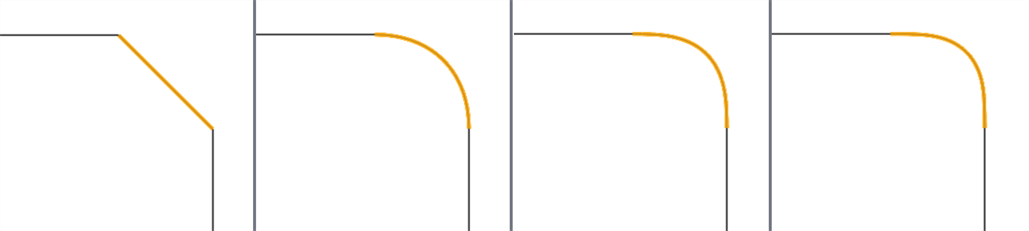
曲线连续性

从左到右：G0（匹配位置）、G1（匹配切线）、G2（匹配曲率）、G3（匹配流动）

将其扩展到曲线之外，可以在 2 个曲面之间创建曲面，并以相同的方式匹配其起点和终点连续性：

曲面连续性

从左到右：G0（匹配位置）、G1（匹配切线）、G2（匹配曲率）、G3（匹配动）

使用曲线/曲面分析工具分析曲线或曲面连续性时，您可以看到，每匹配一次渐进连续性，曲线/曲面之间的连接就会变得更平滑，并显示出更平滑的曲率梳。由于直线没有曲率，因此无法使用“曲线/曲面分析”来分析 G0（匹配位置）。

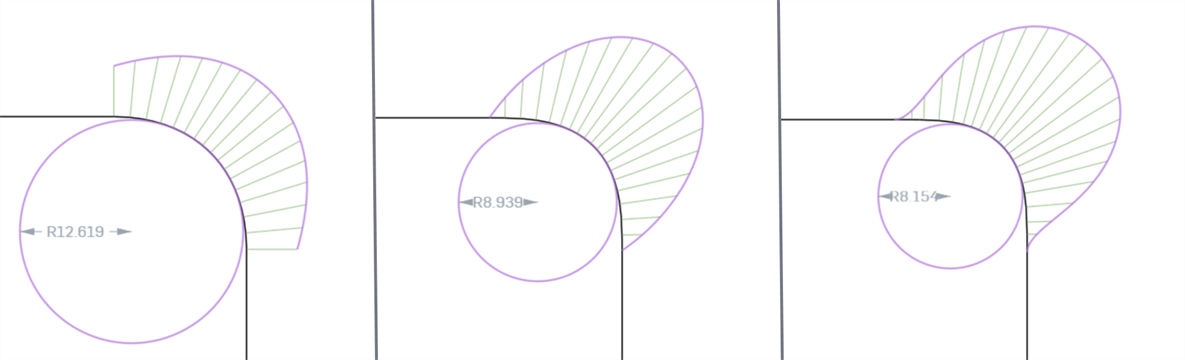
连续性的曲线/曲面分析

从左到右：G1（匹配切线）、G2（匹配曲率）、G3（匹配流动）

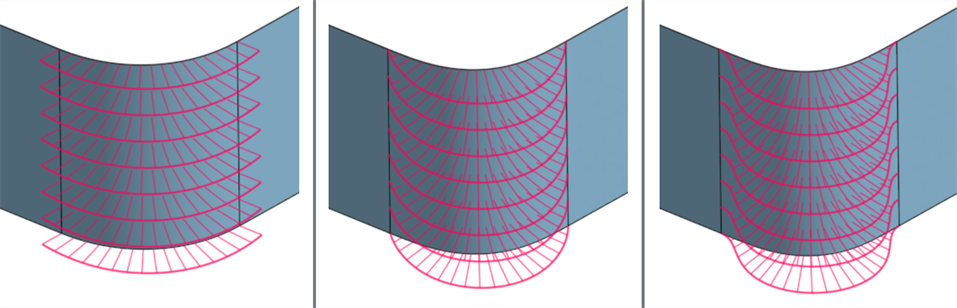
分析曲面连续性

从左到右：G1（匹配切线）、G2（匹配曲率）、G3（匹配流动）

使用斑马条纹工具分析曲线或曲面连续性时，每匹配一次渐进连续性，曲线/曲面之间的连接就会变得更平滑。当您从 G0（匹配位置）上升到 G2（匹配连续性）时，曲面边的斑马条纹变得越来越光滑：

斑马条纹用于分析连续性

从左到右：G0（无连续性）、G1（匹配切线）和 G2（匹配曲率）

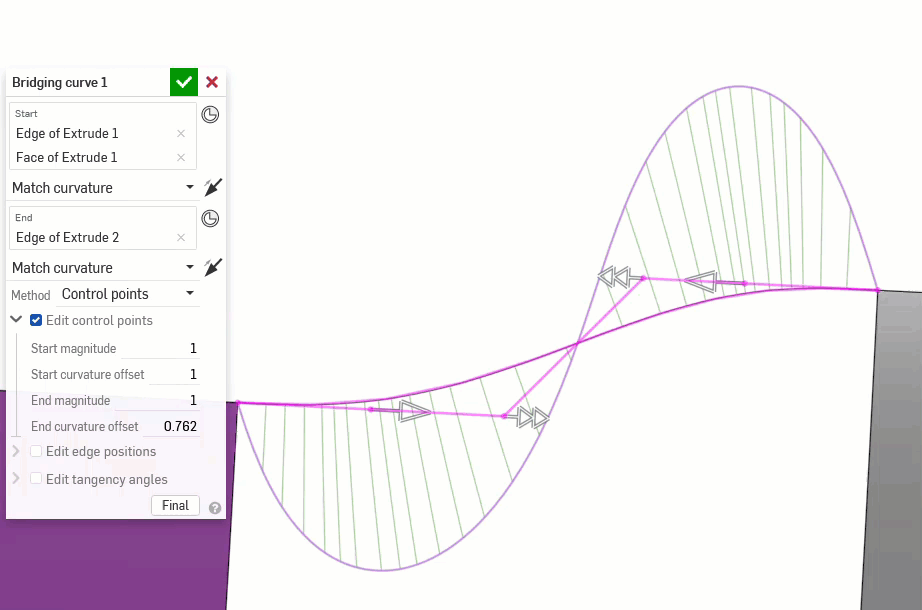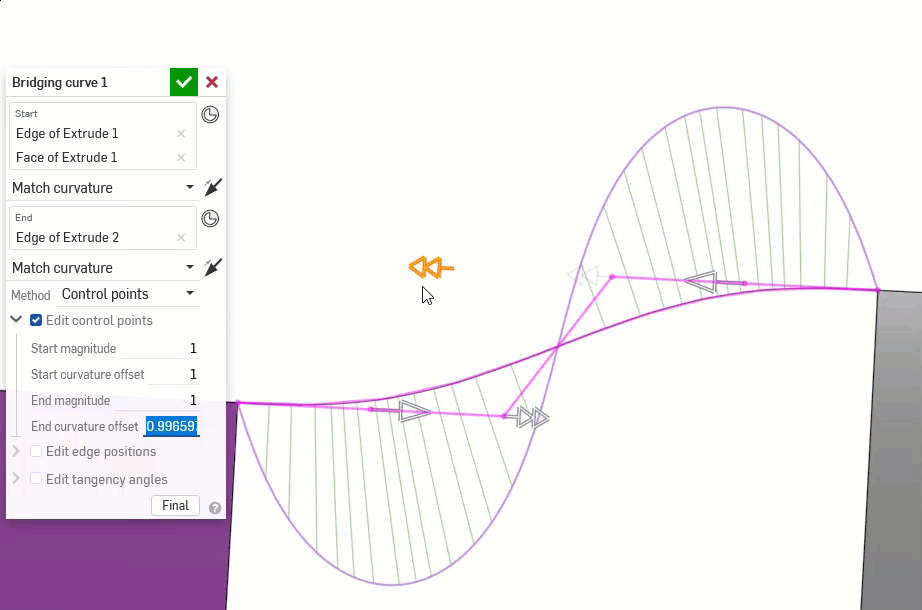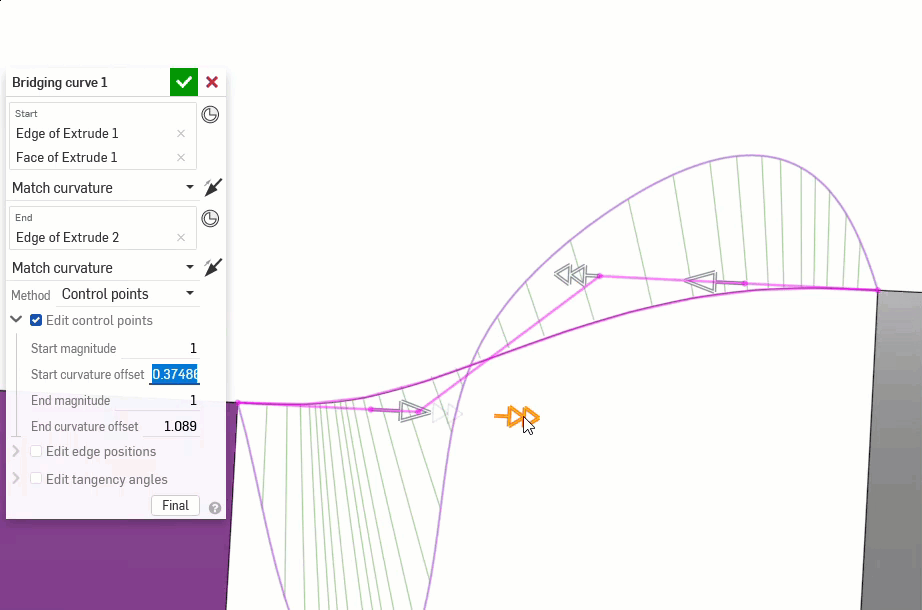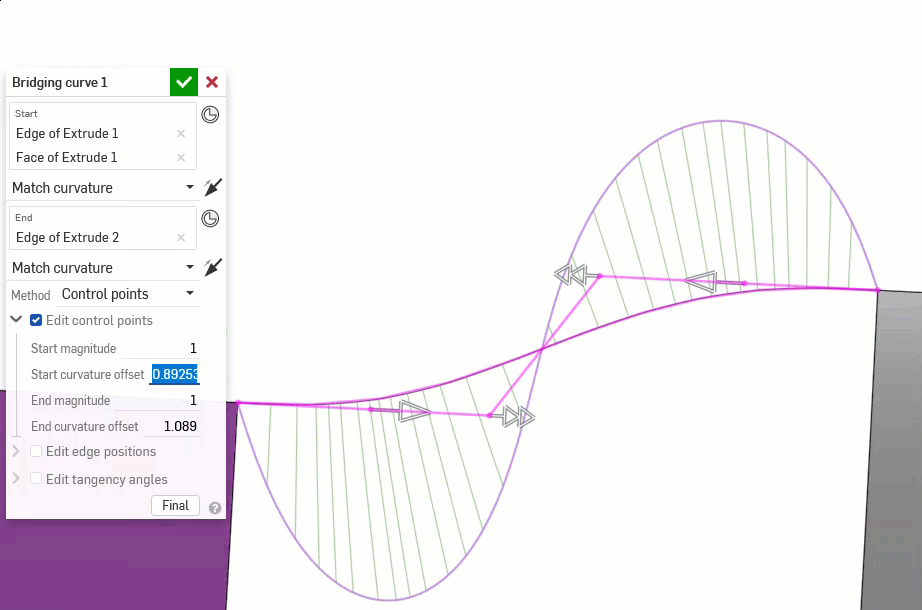
以下示例说明了另外两条非线性曲线之间的桥接曲线上的连续性。桥接曲线为洋红色。第一列显示“桥接曲线”对话框和连续性选择以及结果（并启用“编辑控制点”），中列显示禁用编辑控制点的桥接曲线，最后一列显示所有曲线的“曲线/曲面分析”：

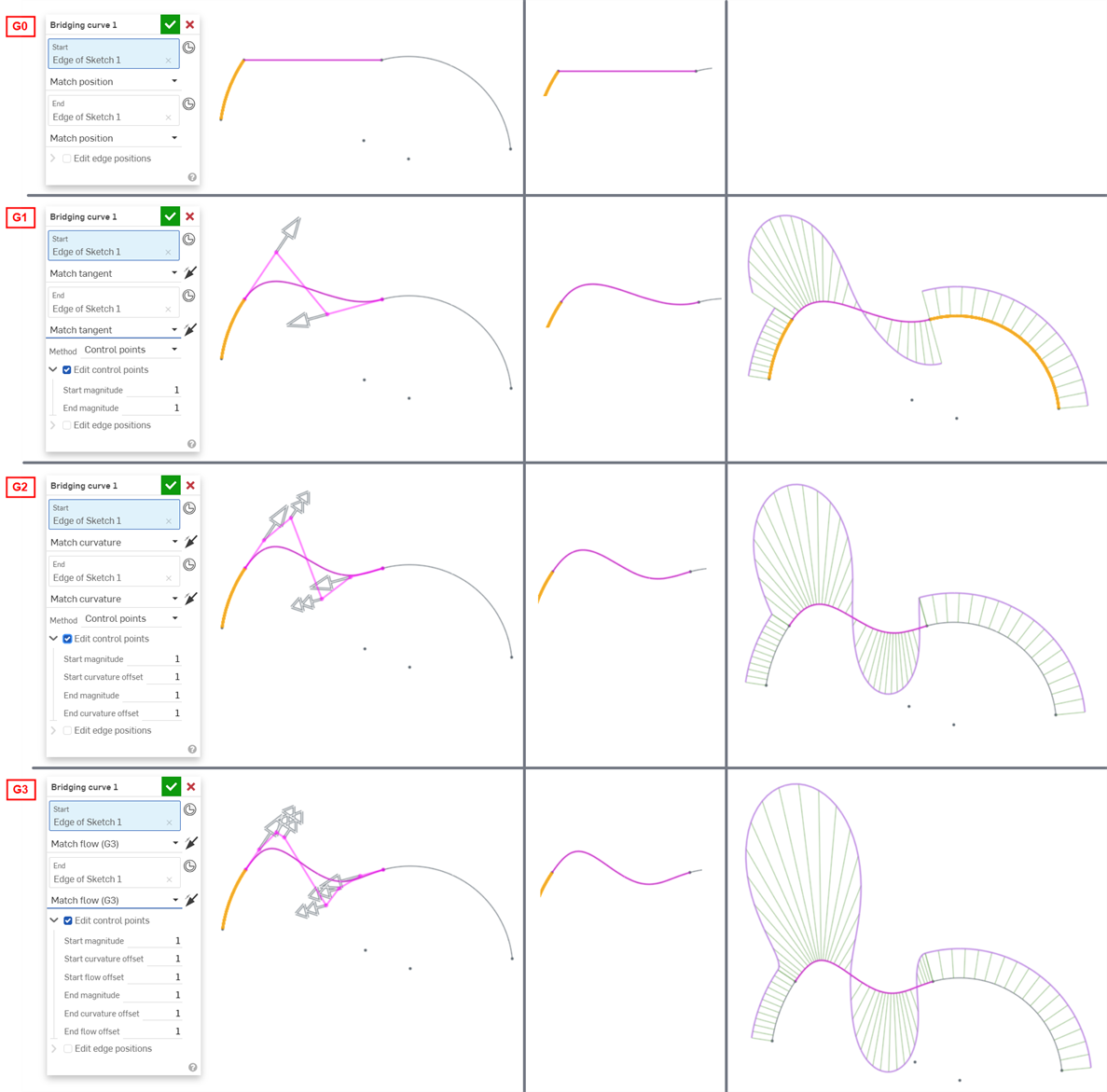
2 条非线性曲线之间的桥接曲线上的连续性示例

为模型中的曲线和曲面连接选择的连续性完全取决于每个交汇点/边所需的连续性级别。曲面连续性没有对错之分。

此外，更高的连续性要求更多的控制点才能执行。G0 只需要一个控制点（端点），G1 需要两个，G2 需要三个，G3 需要四个。一条两端都受到 G3 约束的 Bezier 曲线需要至少八个控制点，每端四个。

控制值（控制点）和连续性

使用曲面建模需要额外的步骤来创建高质量的曲面，这些步骤可以提高性能、避免缺陷并简化复杂曲面的创建。

  • 曲线/曲面分析 - 在 Part Studio 中可视化和分析草图上的曲率。单击 Shift+C，右键单击草图、零件或曲面，或单击界面右下角的“显示分析工具”图标 ()，访问曲线/曲面分析对话框。

    这些工具显示曲率梳（沿边或面的某个点的曲率强度）和控制点网格。理想情况下，曲率梳应平稳增加或减少。

    以下示例在没有评估工具的情况下看起来不错，但是当启用“曲率/曲面分析”时，曲率会出现极大的波动（尤其是左下方的红色 U 方向）。外步边尤其成问题（右下方）：

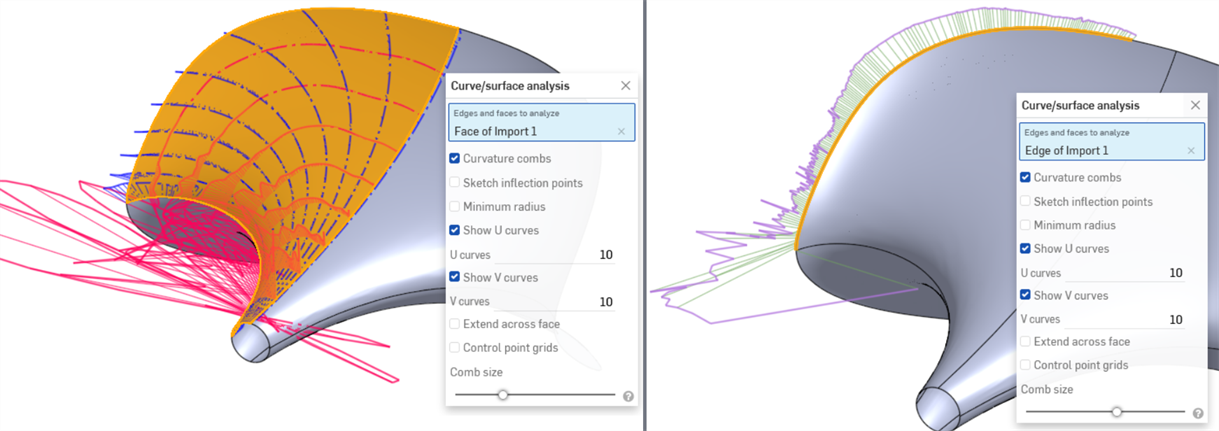
    曲线分析示例

    此外，控制点网格是衡量曲面复杂度的指标。控制点的流量和密度可以说明控制点过多的模型：

    曲线分析密集控制点网格示例

  • 斑马条纹和颜色表 - 斑马条纹表示条纹空间在Part Studio或装配体中的当前模型、面或曲面上的反射。这使您可以查看边和面的曲率是否一致且连续。通过界面右下角的“显示分析工具”图标 () 访问斑马条纹。

    斑马条纹与 G0 或位置连续性不匹配。在 G1 或切线连续性中，它们直接在边上匹配，但会急剧发散。在 G2 或曲率连续性中，斑马条纹平滑地穿过边（如下图所示）。斑马条纹还可以让您看到曲面的缺陷或瑕疵（如下图右所示）：

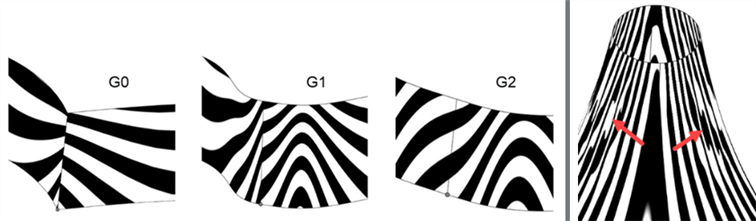
    斑马条纹示例

  • 曲率颜色表 - 通过在 Part Studio 的面或曲面上应用您选择的颜色渐变，可以对曲率进行更深入的研究。调整颜色渐变的比例，从不同类型的色彩映射表中进行选择，以获得最佳的视觉表现效果，从而辨别曲面连续性和边之间的过渡。

    最常见的颜色表曲率选项是“高斯”，它有助于确定曲面曲率是否存在局部缺陷或剧烈变化。使用高斯曲率观察，在上面的斑马条纹图像中检测到的波纹更为明显：

    带有高斯曲率的曲率颜色表

  • 二面角分析 - 通过选择界面右下角的“显示分析工具”图标 () 来访问“二面角”分析。这将显示共享边上的 2 个曲面的法线之间的角度。如果角度为零，则两个曲面在沿边的该位置至少相切。在下面的示例中，二面角有意在曲线另一端从硬折痕变为平滑的切线混合：

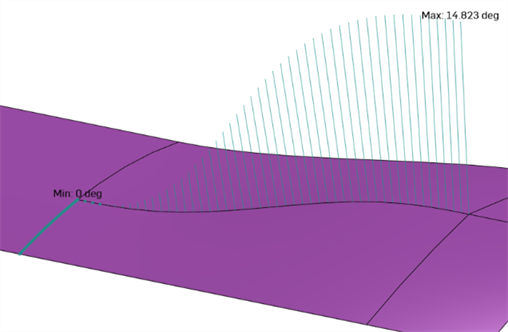
    二面体分析示例

  • 亮显边界边 - 用红色亮显所有开放的边。从“视图”立方体下方的“相机和渲染选项”下拉菜单 () 中访问“亮显边界边”。当您尝试识别曲面中的任何开放区域以形成实体时，这很有用。

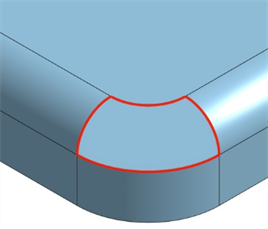
    亮显边界边示例

  • 面相切角度 - 面切角（一种测量工具）可快速反馈接近面的曲线在其端点处是否相切。选择面。切线角度显示在测量工具的左侧。这对于在完成放样或边界曲面之前测试连续性很有用：

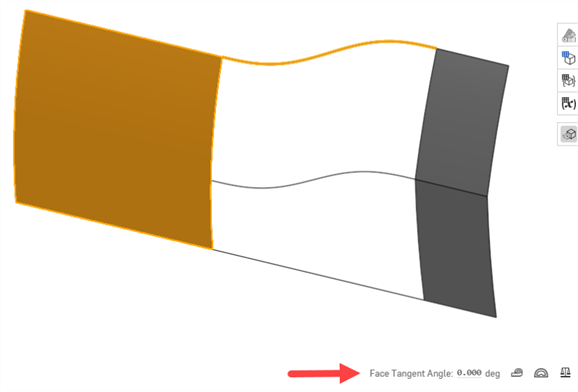
    面切角示例

  • 以高质量模式查看 - 为视图开启最高质量的镶嵌，对于识别曲线缺陷和准确评估连续性至关重要。从“视图”立方体下方的“相机和渲染选项”下拉菜单 () 中以高质量模式查看。

  • 使用边/切线边着色 - 有助于更清晰地查看边连续性。从“视图”立方体下方的“相机和渲染选项”下拉菜单 () 中访问这两个选项。

  • 边界曲面 - 某些特征几乎无法控制曲线以创建曲面，从而过于复杂并降低曲面质量。边界曲面提供对 U 和 V 方向曲线的完全控制。合成曲面仅与输入曲线一样复杂。“放样”、“扫掠”和“填充”特征可在一个或两个方向上创建无法控制的曲线，从而使曲面变得复杂。

    例如，使用“边界曲面”和“扫掠”来构建相同的曲面。扫描沿路径沿 V 方向形成曲线，从而形成过于复杂的曲面：

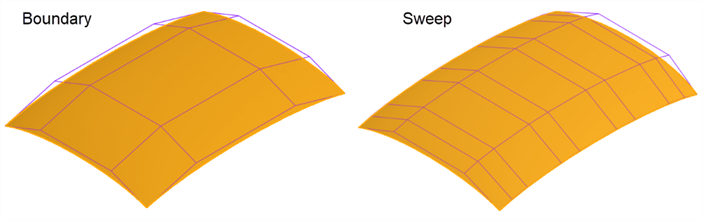
    边界曲面和扫掠示例

    使用“边界曲面”和“扫掠”构建相同的曲面。“放样”在两个方向上创建了密集的控制点网格：

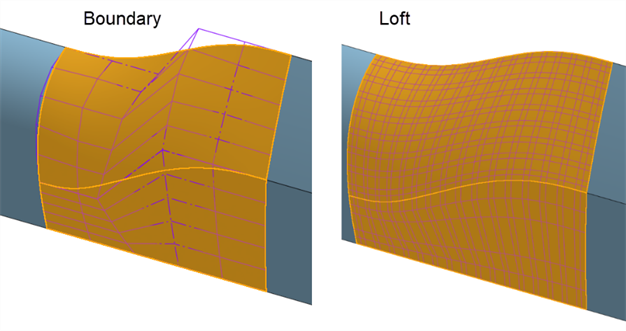
    边界曲面和放样示例

  • 填充 - 填充曲面上的小孔补丁。使用“填充”后，评估生成的曲面以确保曲面质量。在下面的示例中，“填充”向底部添加了一条波纹。“放样”创建了更好的控制点网格，没有波纹，但是“边界曲面”曲面可创建最平滑、最稳定的结果：

    填充示例

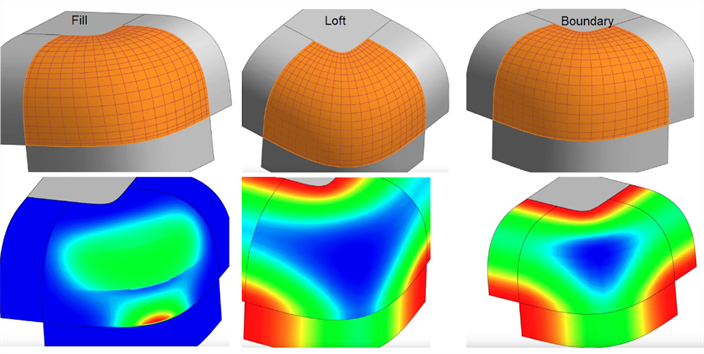
  • 面混合和圆角 –“面混合”和“圆角”可创建类似于投影或分割操作的复杂边。由于这些特征的复杂性，“面混合”和“圆角”创建的边失效和出现瑕疵的可能性更高。由于这通常是装饰性的，因此最好为虚角构建曲面并在最后添加以下特征：

    面混合和圆角示例

  • 使用 Bezier 代替样条 - 样条在曲线上定义了点，在起点和端点上定义了控制柄。Bezier 沿控制多边形偏移量定义了控制点。Bezier 曲线平滑增减，没有连续性中断：

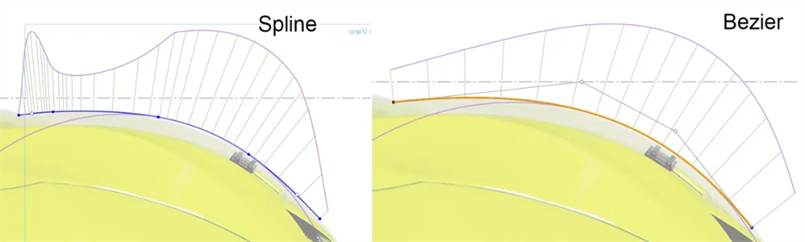
    样条与 Bezier 特征示例

  • 保持曲线的简单性 - 使用 Bezier 工具，从 3 或 4 个控制点（包括端点）开始。尽可能少地添加样条点。

    • Bezier 曲线的度数是控制点数减去 1。Bezier 通常应为 3、5 或 7 度。最好将单条 Bezier 曲线的度数限制为 7，因为在更高的度数下数学计算会变得非常复杂。移动一个控制点会影响整条曲线，如果不引入缺陷，就很难调整更高的曲线。

    • 使用稳定的控制点流来确保曲率的平稳变化，不会发生意外的强度变化。

      以下是曲线控制点位置不当的几个示例。第一个点在第一点和第二点之间有一个锯齿（由圆圈勾勒出）。第二个控制点位于曲线的上方和下方。只有当您打算向曲线添加拐点时，才适合更改将控制点放在哪一边。第三个控制点之间的间距不平滑。该点与其他点的间距有很大不同（如下箭头所示）：

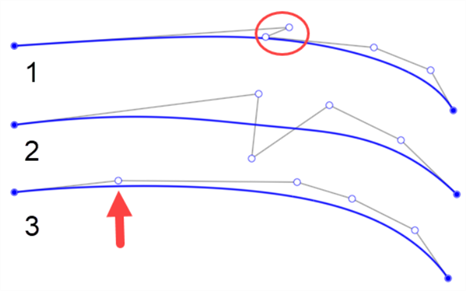
      Bezier 控制点示例

  • 避免使用修剪过的边或投影的曲线进行构建 - 由于它们是由修剪操作或具有许多跨度（分段打结在一起）的 3 度（立方）样条的投影生成的，因此用它们构建的任何东西都更加复杂和不完美。

    例如，当直接从修剪曲面的边（左下方）创建直纹曲面时，此处的曲面具有更密集的控制点网格。相反，过度建造两个曲面，并使用相互修剪来修剪交点处多余的部分（右下方）：

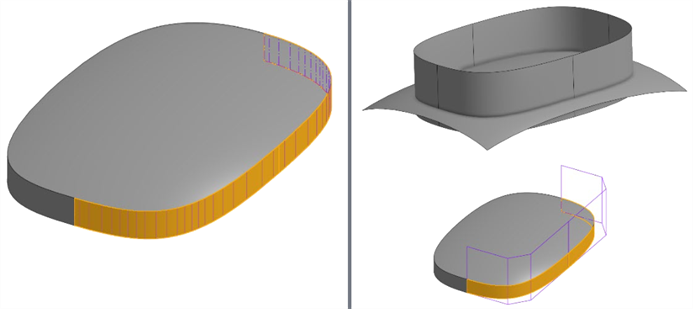
    修剪边示例

    查看桥接曲线而不是投影曲线能否以较低的复杂度构建相同的几何体图元。桥接曲线是 Bezier 曲线，视终端条件而定，最高可达5度。

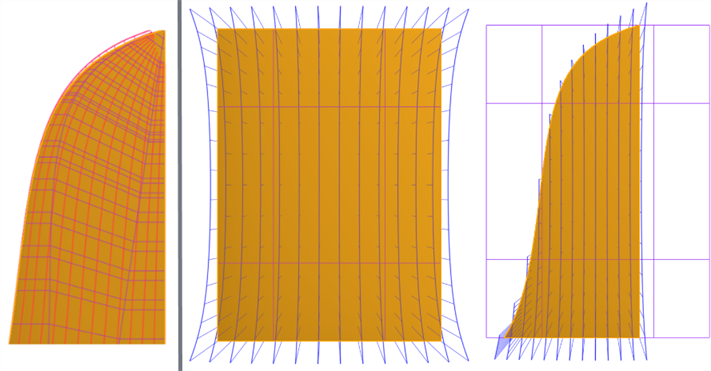
  • 目标是使用四边曲面 - 四边曲面具有最一致的控制点网格。如果创建的曲面没有四条边会导致奇点（退化）或间隔不规则的控制点（如左下方所示）。使用“分割”特征的参考曲面会过度建造和修剪曲面。这样可以创建具有不同边轮廓的曲面，同时保持一致的控制点网格（如右下方所示）：

    控制点一致性示例

  • 尽可能使用对称性 - 对连续性应用约束以确保在中心线上平稳过渡。

    • 在草图中使用具有“切线”或“曲率”约束的参考线。

    • 在 3D 模型中，添加参考曲面以帮助保持生成的曲面的连续性。

  • 使用快捷菜单和热键 - 使用 shift+c（曲线/曲面分析）、shift+d（二面角分析）和 shift+r（以高质量模式查看）。您也可以在“我的帐户 > 首选项> 快捷键工具栏”下自定义“快捷键”工具栏。

这列出了曲面特征工具的集合。这不是一份详尽的清单。对曲面建模时可以使用其他特征工具。有关其他信息，请参阅曲面。

  • 加厚 - 增加曲面的深度。通过赋予曲面厚度并将其转换为实体、在现有零件或曲面中添加或移除材料，或者在其路径中与零件相交来创建新零件或修改现有零件。
  • Enclose - Create a part by selecting all boundaries surrounding an empty space to form a solid. Use any set of surfaces and solids (including planes and faces) that intersect each other or connect at a boundary to create a volume. Create a new part or modify an existing one by adding, removing, or intersecting parts.
  • 圆角 - 使尖锐的内部和外部边变圆，并通过选择“边圆角”定义为标准固定半径、或更样式化的圆锥或变量。或者，可选择应用全圆角，以在两条相对边之间创建一个或多个面的无缝融合。
  • 面混合图标面混合 - 圆滑化锐化连接或不相连的内部和外部面，以在面之间创建无缝混合，或者分离混合以创建新面，定义半径或恒定宽度。进一步定义混合横截面（滚球或扫掠轮廓）、对称性、控制、修剪、约束和界限。
  • 删除面 - 从零件中移除几何图元。选择是否修复周围的面（通过延伸面，直到它们相交）、封口空心或保持空心开放。如果没有零件的参数化历史记录（导入的零件常常出现这种情况），此直接编辑工具特别方便。
  • 移动面 - 平移、旋转或偏移一个或多个选定面。如果没有零件的参数化历史记录（导入的零件常常出现这种情况），此直接编辑工具特别方便。
  • 替换面 - 修剪面或将面延伸到新曲面。如果没有零件的参数化历史记录（导入的零件常常出现这种情况），此直接编辑工具特别方便。
  • 偏移曲面 - 通过偏移现有面、曲面或草图面域创建新曲面。将偏移距离设置为 0 可在原位创建一个副本。
  • 放样特征图标边界曲面 - 创建或添加由其边界轮廓指定的曲面。
  • 填充 - 通过定义边界创建曲面（或从曲面创建零件），并使用边界条件优化曲面（而非要求使用参考曲面）。
  • 移动边界 - 移动曲面的边界边以对其进行延伸或修剪。
  • 直纹曲面 - 从草图区域的现有边或多条边创建新的或额外的直纹曲面。
  • 相互修剪 - 通过延伸交点来修剪两个相邻的曲面以完成修剪。

除曲面处理工具外，曲线还用于创建曲面的基本构件。

这列出了曲线特征工具的集合。这不是一份详尽的清单。操作曲线时可以使用其他特征工具。

  • 草图工具 - 草图工具栏中的工具，例如线、拐角矩形、中心点矩形、中心点圆、三点圆、切线弧、三点弧、三点弧、样条、点和构造，用于在 Part Studio 中创建草图。
  • 螺旋 - 使用圆锥形或圆柱面、嵌合连接器的单轴或 z 轴或圆形边创建螺旋。
  • 3D 拟合样条-通过一系列顶点创建 3D 拟合样条。创建的曲线列在“曲线”下的零件列表中。
  • 投影曲线 - 从两个草图的投影创建曲线（“两个草图”选项）或从面上的曲线的投影创造曲线（“曲线到面”选项）。
  • 桥接曲线 - 创建一条连接任意两个点、顶点或嵌合连接器的曲线。生成的曲线列在特征列表和零件列表中。
  • 复合曲线 - 将多条边显示为一条曲线。选择多条相邻边、草图图元和其他曲线。选择非连续边可能会导致创建多条曲线。针对每条曲线的选择，必须在其顶点处相遇。（曲线列在零件 > 曲线列表中。）
  • 相交曲线 - 在两个或多个曲面或面的相交处创建曲线。所选对象必须相交。
  • 修剪曲线 - 按一定距离修剪或延伸曲线，或修剪或延伸到边界图元。
  • 等斜线 - 在倾斜的面上创建等斜线。在斜面上创建一条等斜线。等斜线所在面的位置与其参考定义相比具有一定坡度。生成的等斜线将列在特征列表和零件清单中。
  • 偏移曲线 - 通过偏移周围面的边来创建、延伸和/或分割新曲线。
  • 等参曲线 - 创建沿 U 或 V 方向的面或曲面延伸的平滑曲线。
  • 编辑曲线 - 通过选择草图图元或曲线来编辑现有曲线，以应用简化的近似值、提升角度、重新定位控制曲线顶点和/或平面化到任何 2D 平面。

如需更多曲面资源，请访问我们的学习中心。