Modélisation de surfaces
![]()
![]()
![]()
Introduction
Une surface est une représentation unilatérale de l'extérieur d'une pièce qui n'a ni masse ni épaisseur.
La modélisation de surface est une approche de modélisation qui permet aux concepteurs de créer des fonctions géométriques complexes et des formes organiques que les outils de modélisation volumique ne peuvent pas produire seuls. La modélisation de surface est utilisée pour un plus grand nombre de formes et de fonctions de forme libre que la modélisation volumique.
Par exemple, un cube peut être divisé en six faces différentes. Chaque face représente une surface qui entoure le volume pour former le cube. Le surfaçage vous permet de construire chaque face du cube comme une surface individuelle. Une fois les six côtés du cube construits, les surfaces sont additionnées et un volume fermé est créé, formant une pièce solide.
La géométrie de surface est utilisée pour :
-
Créer une pièce solide :
-
À l'aide de la fonction Épaissir, une surface est épaissie pour former une pièce solide.
-
À l'aide de la fonction Entourer, une pièce solide est créée en formant un volume fermé, où chaque arête délimite deux faces.
-
-
Créer la géométrie de la construction (lignes de scission pour les moules, fusion et jonction, lissages et remplissages pour faire correspondre la courbure et la tangence).
-
Remplacer la face d'une pièce solide par une géométrie plus complexe (à l'aide de la fonction Remplacer la face).
La continuité des courbes et des surfaces est une mesure de la régularité de la jonction entre 2 courbes ou 2 surfaces où elles se rejoignent. Au fur et à mesure que les courbes et les surfaces sont créées pour créer des modèles géométriques, la continuité revêt une importance croissante pour aboutir à la forme organique la plus fluide ou la plus continue.
La désignation G (ou géométrie) est utilisée pour déterminer la continuité courbe/surface (G0 à G3). Dans Onshape, ces désignations sont en corrélation avec les options de correspondance de nombreuses fonctions de courbes et de surfaces (par exemple, jonction de courbes, congé, raccordement de faces, etc.). Ces classifications de continuité sont décrites ci-dessous, avec leurs définitions :
-
G0 (Correspondance de position) - Les 2 courbes/surfaces sont mises en correspondance sur la base de la position. Les deux courbes/surfaces partagent une position commune au niveau du point de jonction.
-
G1 (Correspondance de tangence) - Les 2 courbes/surfaces sont mises en correspondance sur la base de la tangence. Les deux courbes/surfaces se touchent et partagent un angle commun qui est égal aux deux extrémités. Un congé est un bon exemple de ce type de correspondance.
-
G2 (Correspondance de courbure) - Les 2 courbes/surfaces sont mises en correspondance sur la base de la courbure. Les deux courbes/surfaces se touchent, sont tangentes et présentent la même courbure au point où elles se touchent (elles ont toutes deux des rayons identiques).
-
G3 (Correspondance de flux) - Les 2 courbes/surfaces sont mises en correspondance sur la base du flux. Les deux courbes/surfaces se touchent, sont tangentes, ont une courbure similaire et montrent l'ampleur de la variation de la courbure sur la longueur de la courbure (flux).
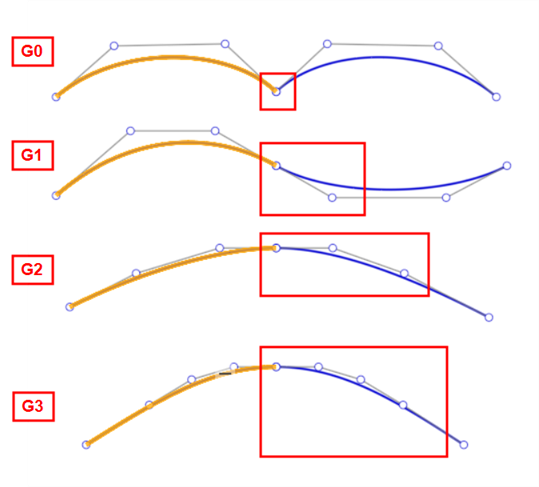
À l'aide de la fonction Courbe de jonction, vous pouvez créer une courbe de jonction (illustrée ci-dessous en orange) entre deux courbes et faire correspondre sa position de début et de fin, sa tangence, sa courbure et son flux (ou une combinaison des deux ; par exemple, Faire correspondre la position au début et Faire correspondre la courbure à la fin) :
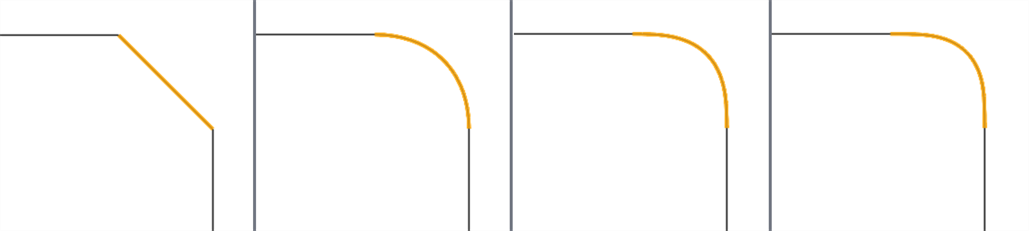
De gauche à droite : G0 (correspondance de position), G1 (correspondance de tangence), G2 (correspondance de courbure), G3 (correspondance de flux)
Au-delà des courbes, vous pouvez créer une surface entre deux surfaces et faire correspondre la continuité de début et de fin de la même manière :

De gauche à droite : G0 (correspondance de position), G1 (correspondance de tangence), G2 (correspondance de courbure), G3 (correspondance de flux)
Lorsque vous analysez la continuité d'une courbe ou d'une surface à l'aide de l' outil d'analyse de courbes/surfaces, vous pouvez constater qu'à chaque correspondance de continuité progressive, les connexions entre les courbes/surfaces deviennent plus lisses et présentent des champs de courbure plus lisses. G0 (Correspondance de position) ne peut pas être analysé à l'aide de l'analyse courbe/surface car une ligne droite ne présente aucune courbure.
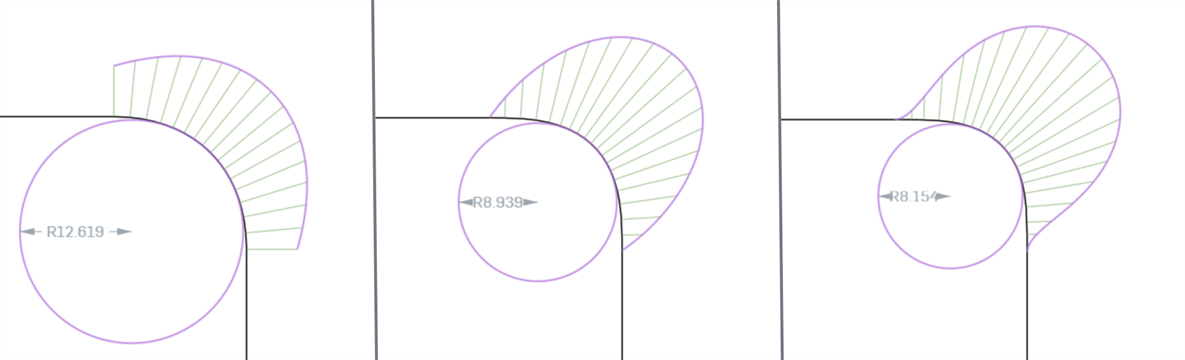
De gauche à droite : G1 (correspondance de tangence), G2 (correspondance de courbure), G3 (correspondance de flux)
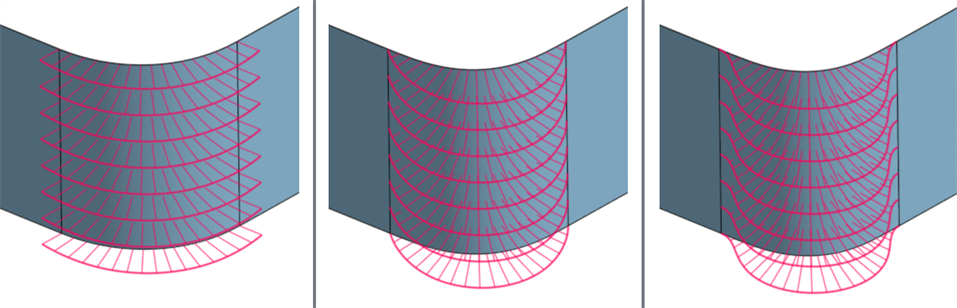
De gauche à droite : G1 (correspondance de tangence), G2 (correspondance de courbure), G3 (correspondance de flux)
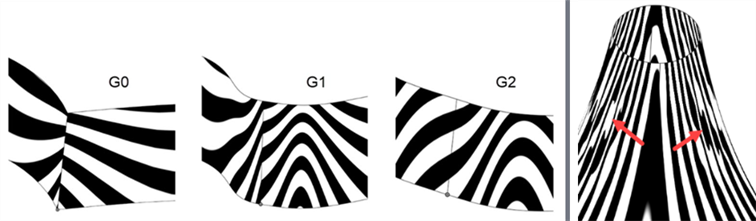
Lors de l'analyse de la continuité d'une courbe ou d'une surface à l'aide de l'outil Rayures zébrées, à chaque correspondance de continuité progressive, la connexion entre les courbes/surfaces devient plus fluide. Les rayures zébrées sur les arêtes de la surface deviennent de plus en plus lisses à mesure que vous passez de G0 (correspondance de position) à G2 (correspondance de continuité) :

De gauche à droite : G0 (aucune continuité), G1 (Correspondance des tangentes) et G2 (Faire correspondre la courbure )
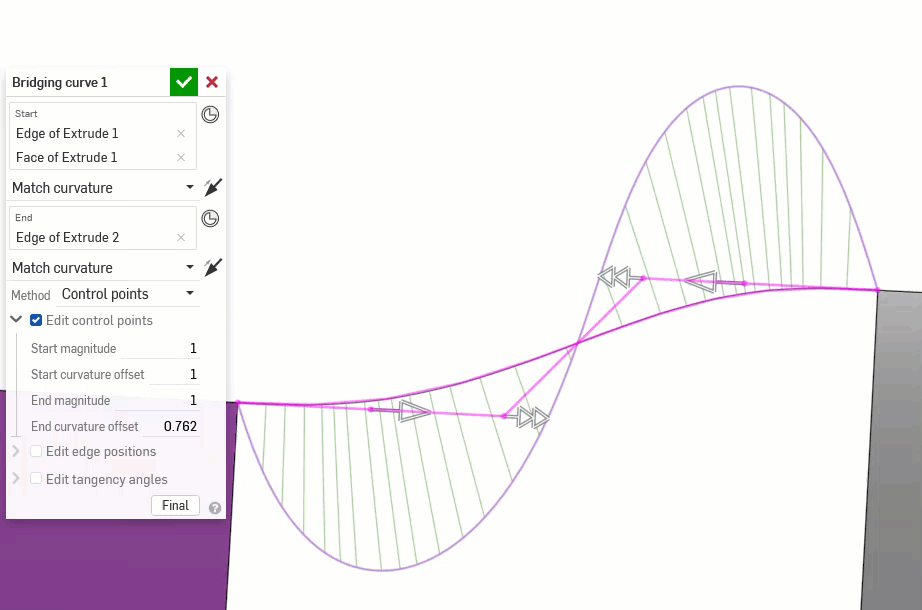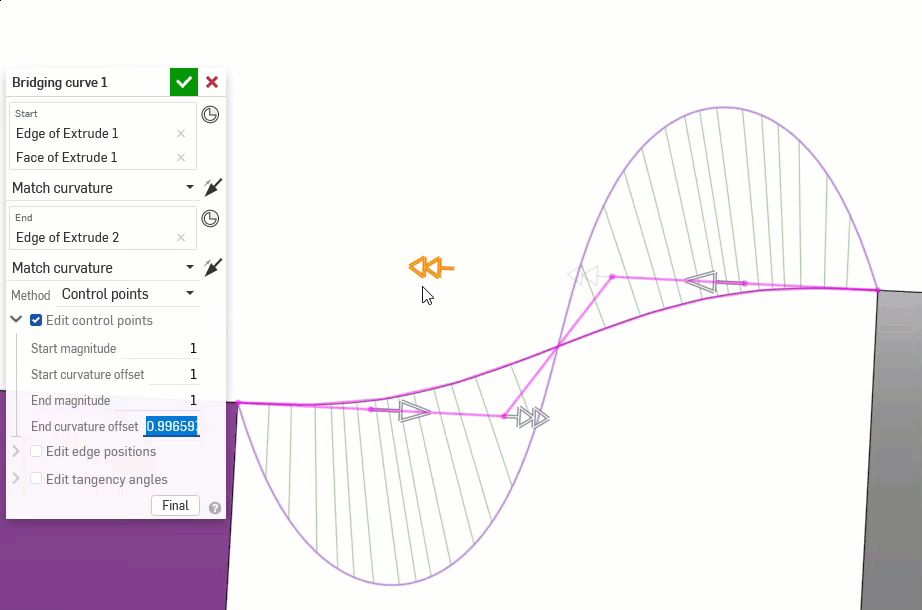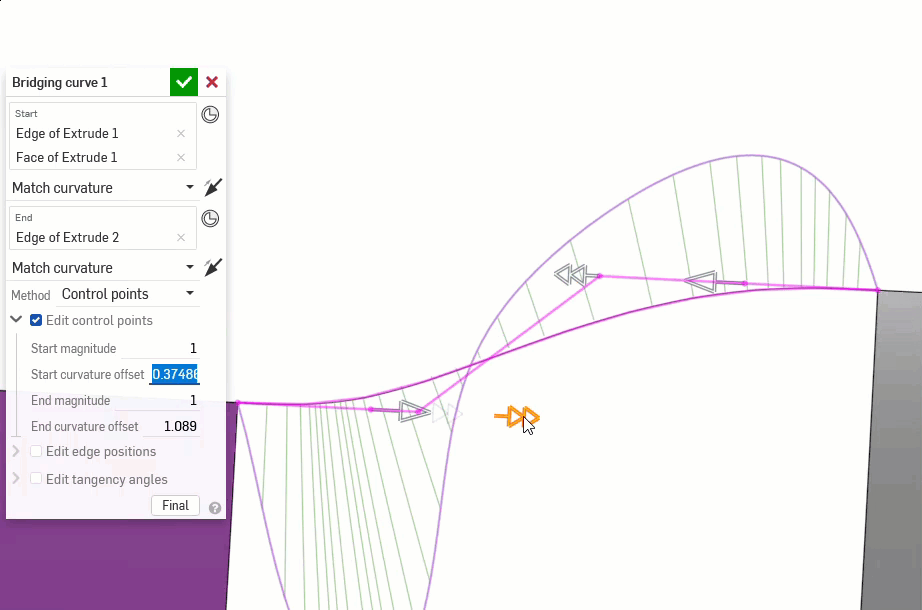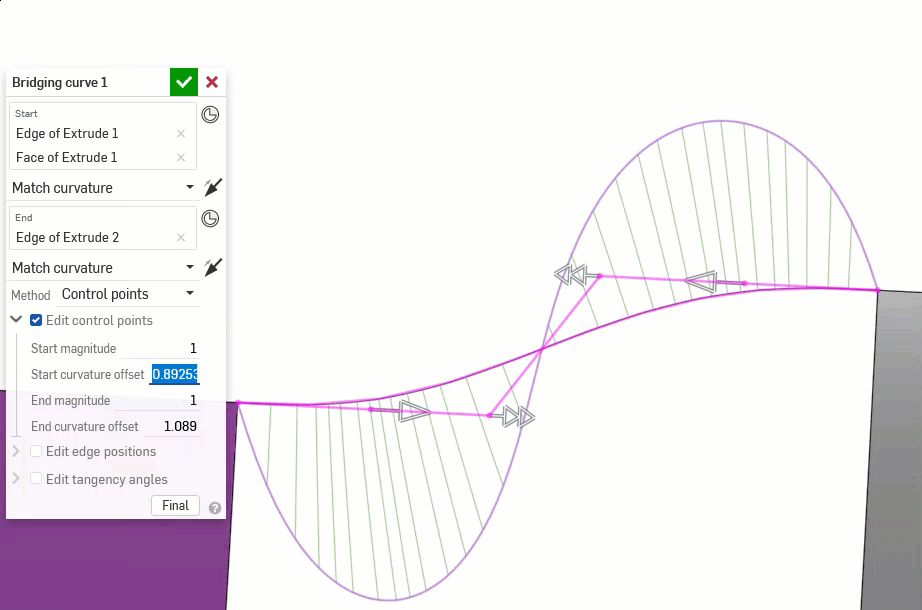
Les exemples suivants illustrent les continuités d'une courbe de jonction entre deux autres courbes non linéaires. La courbe de jonction est colorée en magenta. La première colonne affiche la boîte de dialogue Courbe de jonction et la sélection de continuité avec le résultat (et l'option Modifier les points de contrôle est activée), la colonne du milieu montre la courbe de jonction avec l'option Modifier les points de contrôle désactivée, et la dernière colonne montre l'analyse des courbes/surfaces pour toutes les courbes :
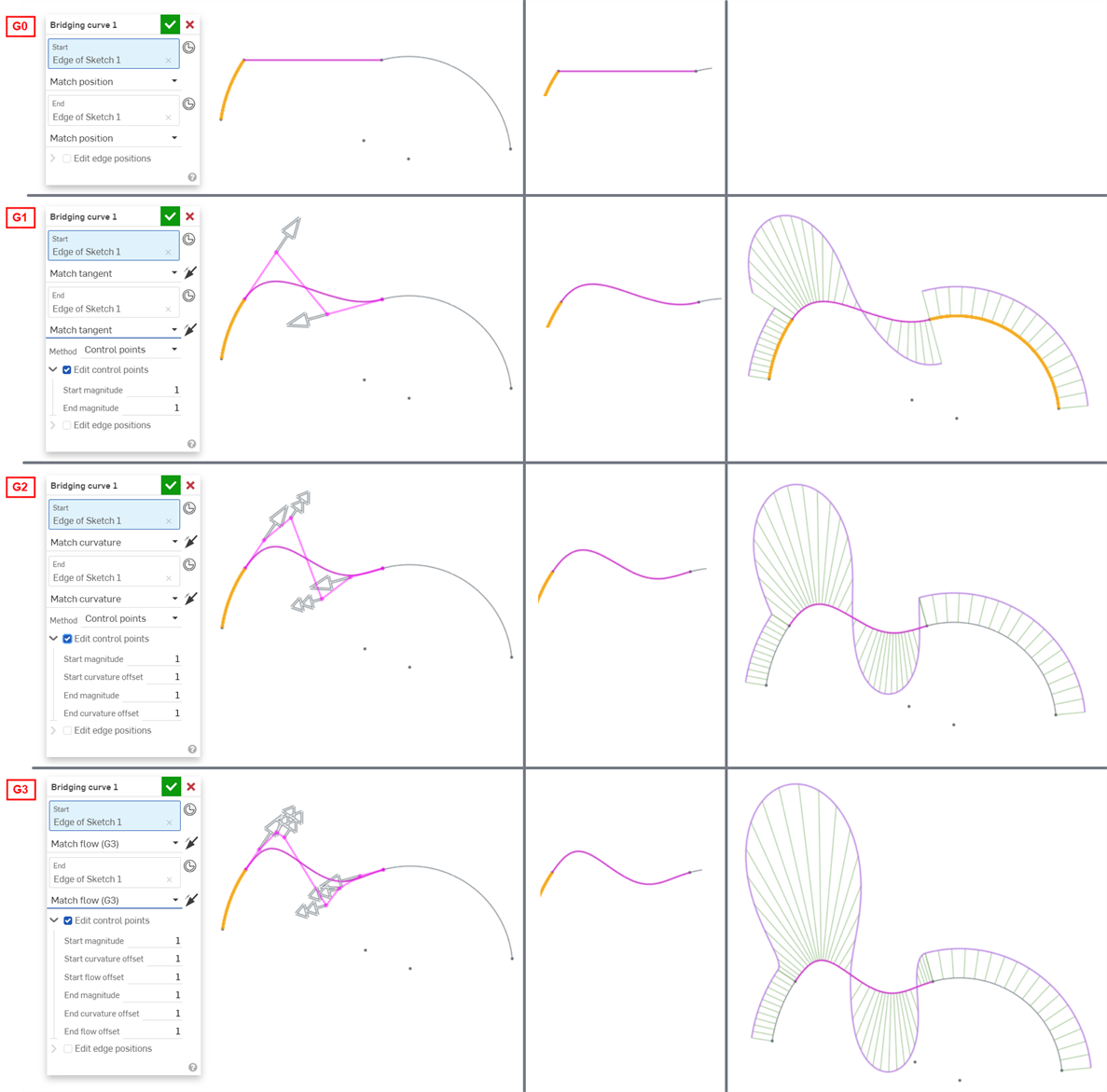
La continuité sélectionnée pour les connexions de courbe et de surface dans votre modèle dépend entièrement du niveau de continuité requis à chaque jonction/arête. Il n'y a pas de bonne ou de mauvaise continuité de surface.
En outre, les ordres de continuité plus élevés nécessitent davantage de points de contrôle pour être appliqués. G0 n'a besoin que d'un seul point de contrôle (le point final), G1 en a besoin de deux, G2 en a besoin de trois et G3 en a besoin de quatre. Une courbe de Bézier soumise à des contraintes G3 aux deux extrémités nécessite au moins huit points de contrôle, quatre pour chaque extrémité.
La modélisation surfacique nécessite le passage par des étapes supplémentaires pour créer des surfaces de haute qualité. Ces étapes augmentent les performances, évitent les imperfections et fluidifient la création de surfaces complexes.
-
Analyse des courbes/surfaces - Visualisez et analysez la courbure sur une esquisse dans un Atelier de pièces. Accédez à la boîte de dialogue Analyse des courbes/surfaces en cliquant sur Shift+C, en cliquant avec le bouton droit sur une esquisse, une pièce ou une surface, ou en cliquant sur l'icône Afficher les outils d'analyse (
 ) dans le coin inférieur droit de l'interface.
) dans le coin inférieur droit de l'interface.Ces outils montrent des champs de courbure (intensité de la courbure en un point donné le long d'une arête ou d'une face) et des grilles de points de contrôle. Idéalement, les champs de courbure devraient augmenter ou diminuer de manière constante.
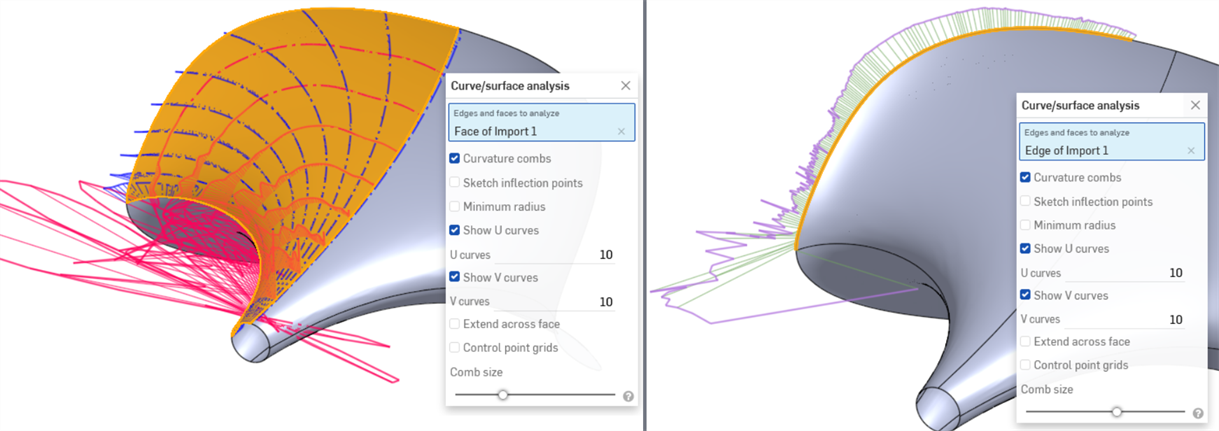
L'exemple suivant semble correct sans outils d'évaluation mais montre des fluctuations extrêmes de courbure (en particulier dans la direction du U rouge en bas à gauche) lorsque l'analyse de courbure/surface est activée. L'arête extérieure est particulièrement problématique (en bas à droite) :
De plus, la grille de points de contrôle est une mesure de la complexité de la surface. Le flux et la densité des points de contrôle peuvent illustrer un modèle comportant trop de points de contrôle :

-
Connection analysis - Assess or report the connection between curves and surfaces in a Part Studio or Sketch. Access the Connection analysis dialog from the Show analysis tools icon (
 ) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
) at the bottom right corner of the interface. Select curves or surfaces to analyze; the dialog box (shown below) populates with results automatically upon selection, along with color coordinated indicators in the graphics area.
-
Rayures zébrées et palette de couleurs - Les rayures zébrées représentent le reflet d'une pièce rayée sur le modèle, les faces ou les surfaces actuels d'un atelier de pièces ou d'un assemblage. Cela vous permet de voir si la courbure sur les arêtes et les faces est alignée et continue. Accédez à Rayures zébrées depuis l'icône Afficher les outils d'analyse (
 ) dans le coin inférieur droit de l'interface.
) dans le coin inférieur droit de l'interface.Les rayures zébrées ne correspondent pas à G0 ou à la continuité de position. En G1 ou en continuité de tangence, ils correspondent directement sur l'arête mais divergent fortement. En G2 ou continuité de courbure, les rayures zébrées traversent doucement l'arête (illustration en bas à gauche). Les rayures zébrées vous permettent également de voir les défauts ou les imperfections de la surface (voir ci-dessous à droite) :
-
Palette de couleurs de courbure - Permet d'étudier plus en profondeur la courbure en appliquant le dégradé de couleur de votre choix sur une face ou une surface dans un Atelier des pièces. Vous pouvez ajuster l'échelle du dégradé de couleurs et choisir parmi différents types de palettes de couleurs pour obtenir la meilleure représentation visuelle afin de discerner la continuité de surface et la transition entre les arêtes.
L'option de courbure de la palette de couleurs la plus courante est la courbure de Gauss, utile pour détecter des imperfections locales ou des changements radicaux dans la courbure de la surface. L'ondulation détectée dans les rayures zébrées ci-dessus est plus apparente lorsqu'elle est observée avec une courbure de Gauss :

-
Analyse dièdre - Accédez à l'analyse dièdre en sélectionnant l'icône Afficher les outils d'analyse (
 ) dans le coin inférieur droit de l'interface. Cela affiche l'angle entre les normales de deux surfaces sur une arête commune. Si l'angle est nul, les 2 surfaces sont au moins tangentes à cet endroit le long de l'arête. Dans l'exemple ci-dessous, le dièdre passe intentionnellement d'un pli dur à un raccordement tangent lisse à l'autre extrémité de la courbe :
) dans le coin inférieur droit de l'interface. Cela affiche l'angle entre les normales de deux surfaces sur une arête commune. Si l'angle est nul, les 2 surfaces sont au moins tangentes à cet endroit le long de l'arête. Dans l'exemple ci-dessous, le dièdre passe intentionnellement d'un pli dur à un raccordement tangent lisse à l'autre extrémité de la courbe :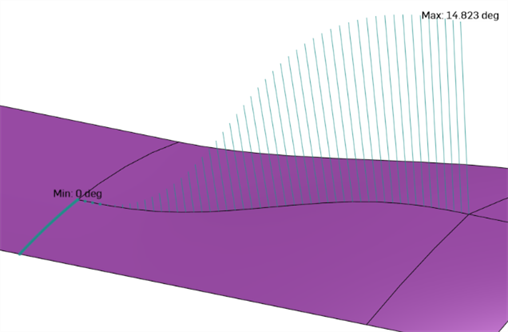
-
Deviation analysis - Display the minimum and maximum deviation between 2 curve chains in a Sketch or Part Studio, or 2 surfaces in a Part Studio.
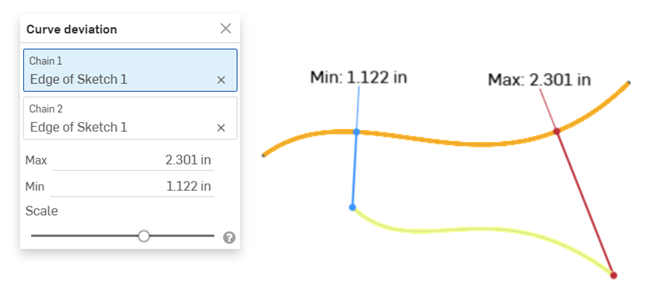
Example showing the Max/Min deviation between two curves
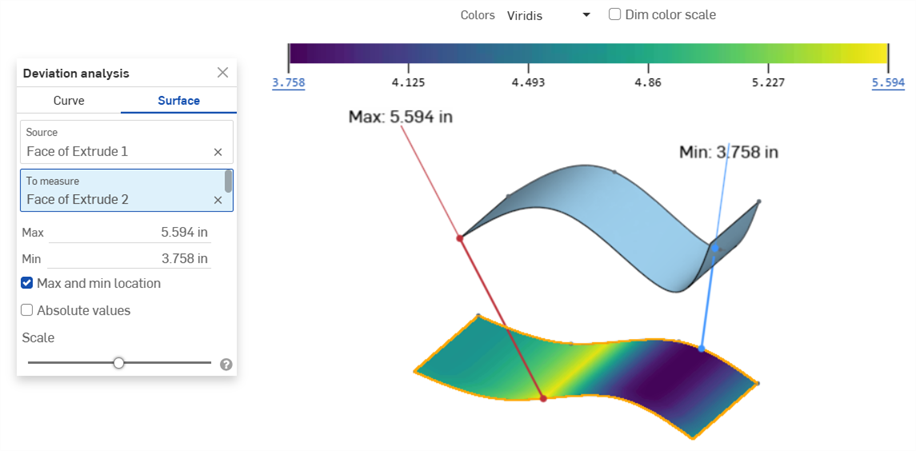
Example showing the Max/Min deviation between a "Source" surface and a surface "To measure"
See Deviation analysis for more information.
-
Reflection analysis - Renders the model in the graphics area with a reflective material and environment image of your preference.
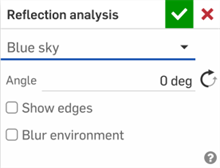

See Reflection analysis for more information.
-
Surligner les arêtes de contour - Surligner les arêtes de contour en rouge. Accédez à Surligner les arêtes de contour à partir de la liste déroulante des options de caméra et de rendu (
 ) située sous le cube d'affichage. Cette option est utile pour identifier les zones ouvertes d'une surface pour former un solide.
) située sous le cube d'affichage. Cette option est utile pour identifier les zones ouvertes d'une surface pour former un solide.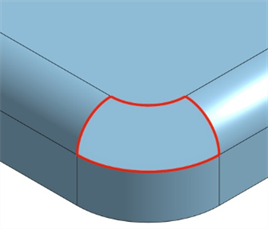
-
Angle de tangence à la face - L'angle de tangence à la face (un outil de mesure) permet de savoir rapidement si une courbe approchant une face est tangente à son extrémité. Sélectionnez la face. L'angle de tangence est affiché à gauche de l'outil de mesure. Cette option est utile pour tester la continuité avant de terminer un lissage ou une surface de contour :
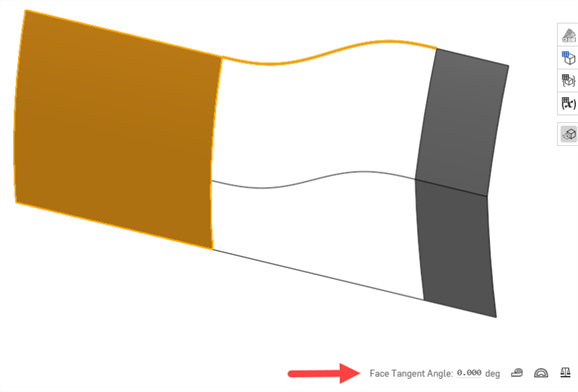
-
Affichage en haute qualité - Active la meilleure qualité de facétisation disponible pour la vue et est essentiel pour identifier les imperfections de la courbe et évaluer la continuité avec précision. Accédez à l'affichage en haute qualité à partir de la liste déroulante des options de caméra et de rendu (
 ) située sous le cube d'affichage.
) située sous le cube d'affichage. -
Ombré avec arêtes/Arêtes tangentes - Utile pour visualiser plus clairement la continuité des arêtes. Accédez à ces deux options depuis la liste déroulante des options de caméra et de rendu (
 ) située sous le cube d'affichage.
) située sous le cube d'affichage.
-
Surface de contour - Certaines fonctions ne permettent que peu de contrôle sur les courbes pour créer une surface, ce qui complique à l'excès et diminue la qualité de la surface. Une surface de contour permet un contrôle complet des courbes de direction U et V. La surface résultante est aussi complexe que les courbes d'entrée. Les fonctions de lissage, de balayage et de remplissage créent des courbes dans une direction ou dans les deux directions qui ne peuvent pas être contrôlées, ce qui complexifie la surface.
Par exemple, la même surface est construite avec une surface de contour et un balayage. Le balayage développe des courbes dans la direction V le long de la trajectoire, créant une surface trop complexe :
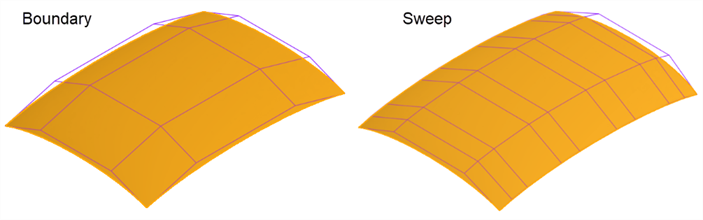
La même surface est construite avec une surface de contour et un lissage. Le lissage crée une grille de points de contrôle dense dans les deux sens :
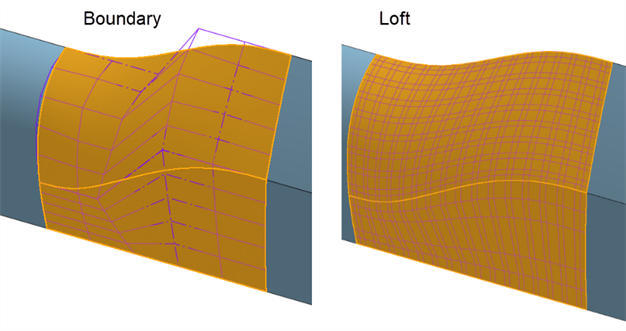
-
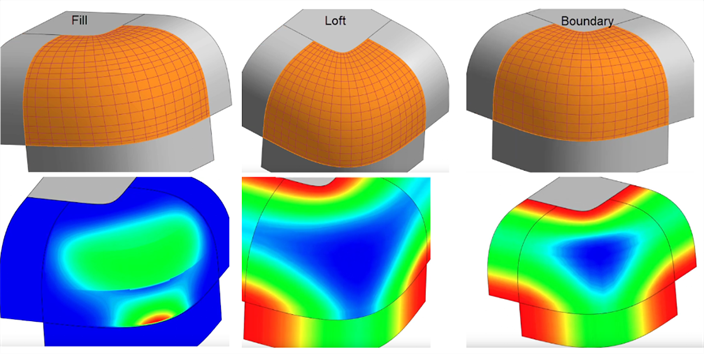
Remplissage - Remplir les petites zones et les petits trous d'une surface. Après avoir utilisé Remplir, évaluez la surface obtenue pour garantir une surface de qualité. Dans l'exemple ci-dessous, le remplissage ajoute une ondulation vers le bas. Le lissage crée une meilleure grille de points de contrôle sans ondulation, mais la surface de contour permet d'obtenir le résultat le plus lisse et le plus cohérent :
-
Combinaison de faces et Congé - La combinaison de faces et le congé créent des arêtes complexes similaires à des projections ou à des opérations de scission. Les arêtes créées sont plus susceptibles d'aboutir à des défauts ou à des imperfections en raison de la complexité de ces fonctions. Comme il s'agit généralement d'une question d'esthétique, il est préférable de construire les surfaces sur des intersections virtuelles et d'ajouter ces fonctions à la fin :

-
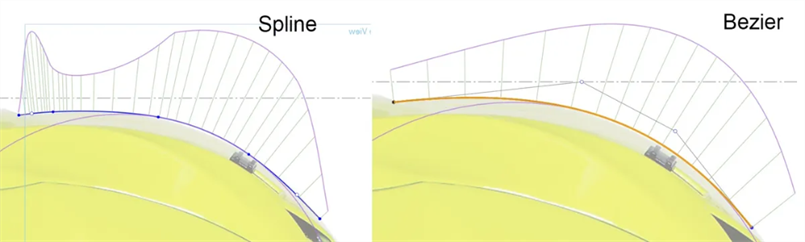
Utilisez des Bézier plutôt que des splines : les splines comportent des points définis le long de la courbe et des poignées aux points de départ et d'arrivée. Les Bézier possèdent des points de contrôle définis le long du polygone de contrôle décalés par rapport à la courbe. Les courbes de Bézier augmentent et diminuent en douceur, sans interruption de continuité :
-
Simplifiez les courbes : utilisez l'outil de Bézier et commencez par 3 ou 4 points de contrôle (y compris les extrémités). Ajoutez le moins possible de points de spline.
-
Le degré d'une Bézier est le nombre de points de contrôle moins 1. Les Bézier doivent généralement être de degré 3, 5 ou 7. Il est préférable de limiter le degré d'une seule courbe de Bézier à 7 car le calcul mathématique devient très complexe à des degrés plus élevés. Le déplacement d'un point de contrôle affecte l'ensemble de la courbe, et les courbes de degré supérieur sont difficiles à ajuster sans introduire d'imperfections.
-
Utilisez un flux constant de points de contrôle pour garantir des changements de courbure en douceur, sans changements d'intensité imprévus.
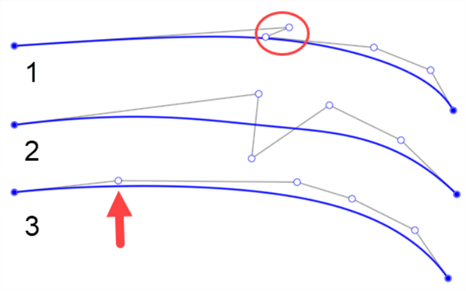
Vous trouverez ci-dessous quelques exemples de courbes dont les points de contrôle sont mal placés. Le premier comporte un zig-zag entre le premier et le deuxième point (délimité par le cercle). Le second comporte des points de contrôle positionnés au-dessus et en dessous de la courbe. Il est recommandé de changer le côté sur lequel vous placez les points de contrôle uniquement si vous souhaitez ajouter une inflexion à la courbe. Le troisième exemple montre un espacement irrégulier entre les points de contrôle. L'espacement entre les points est radicalement différent (indiqué par la flèche ci-dessous) :
-
-
Évitez de construire à partir d'arêtes ajustées ou de courbes projetées. Comme celles-ci sont réalisées à partir d'opérations d'ajustement ou de projection comportant de nombreuses portées (segments noués ensemble) de splines de degré 3 (cubiques), tout ce qui est construit à partir de celles-ci est plus complexe et moins parfait.
Par exemple, la surface présente ici une grille de points de contrôle plus dense lors de la création d'une surface réglée directement à partir d'une arête d'une surface ajustée (en bas à gauche). Surconstruisez plutôt les deux surfaces et utilisez un ajustement mutuel pour réduire l'excédent à l'intersection (en bas à droite) :
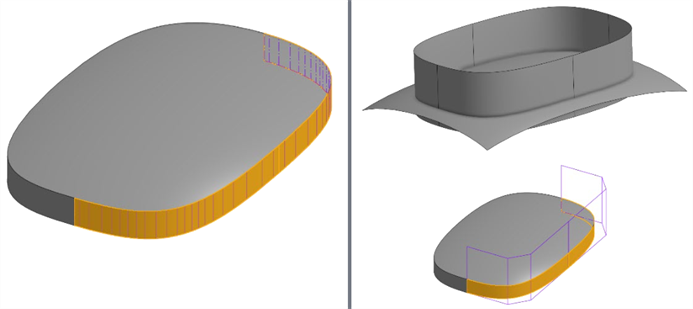
Plutôt que des courbes projetées, voyez si les courbes de jonction peuvent créer la même géométrie avec moins de complexité. Les courbes de jonction sont des courbes de Bézier qui peuvent atteindre 5 degrés, selon les conditions de fin.
-
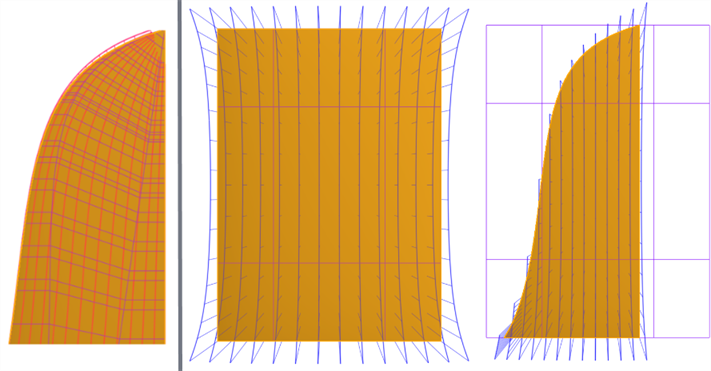
Essayez d'utiliser des surfaces à quatre côtés - Les surfaces à quatre côtés ont la grille de points de contrôle la plus cohérente. La création d'une surface sans quatre côtés entraîne des singularités (altérations) ou des points de contrôle irrégulièrement espacés (illustrés en bas à gauche). Surconstruisez et ajustez la surface avec une surface de référence à l'aide de la fonction Scinder. Cela permet de créer des surfaces avec des profils d'arête différents, tout en maintenant une grille de points de contrôle cohérente (illustrée ci-dessous à droite) :
-
Utilisez la symétrie dans la mesure du possible - Appliquez des contraintes pour la continuité afin de garantir une transition en douceur sur l'axe de symétrie.
-
Utilisez des lignes de référence dans une esquisse avec des contraintes de tangence ou de courbure.
-
Dans un modèle 3D, ajoutez des surfaces de référence pour assurer la continuité de la surface générée.
-
-
Utilisez les menus contextuels et les touches de raccourci - Utilisez shift+c (analyse des courbes/surfaces), shift+d (analyse dièdre) et shift+r (Afficher en haute qualité). Vous pouvez également personnaliser la ou les barres d'outils de raccourcis sous Mon compte > Préférences > Barres d'outils de raccourcis.
Cette liste répertorie la collection d'outils de fonction de surface. Elle n'est pas exhaustive. Des outils de fonction supplémentaires peuvent être utilisés lors de la modélisation de surfaces. Voir Surfaçage pour plus d'informations.
-
 Épaissir - Ajoutez de la profondeur à une surface. Créez une nouvelle pièce ou modifiez une pièce existante en donnant de l'épaisseur à une surface et en la convertissant en un solide, en ajoutant ou en supprimant du matériau d'une pièce ou d'une surface existante, ou en recoupant des pièces dans son tracé.
Épaissir - Ajoutez de la profondeur à une surface. Créez une nouvelle pièce ou modifiez une pièce existante en donnant de l'épaisseur à une surface et en la convertissant en un solide, en ajoutant ou en supprimant du matériau d'une pièce ou d'une surface existante, ou en recoupant des pièces dans son tracé. -
 Entourer - Créez une pièce en sélectionnant toutes les limites entourant un espace vide pour former un solide. Utilisez n'importe quel ensemble de surfaces et de solides (y compris des plans et des faces) qui se croisent ou se connectent au niveau d'un contour pour créer un volume. Créez une nouvelle pièce ou modifiez une pièce existante en ajoutant, en supprimant ou en croisant des pièces.
Entourer - Créez une pièce en sélectionnant toutes les limites entourant un espace vide pour former un solide. Utilisez n'importe quel ensemble de surfaces et de solides (y compris des plans et des faces) qui se croisent ou se connectent au niveau d'un contour pour créer un volume. Créez une nouvelle pièce ou modifiez une pièce existante en ajoutant, en supprimant ou en croisant des pièces. -
 Appliquer un congé - Arrondissez les arêtes intérieures et extérieures tranchantes et définissez-les comme rayon constant standard, conique plus stylisé ou variable en sélectionnant Congé d'arête. Vous pouvez éventuellement appliquer un congé arrondi complet pour créer un mélange homogène d'une ou de plusieurs faces entre deux côtés opposés.
Appliquer un congé - Arrondissez les arêtes intérieures et extérieures tranchantes et définissez-les comme rayon constant standard, conique plus stylisé ou variable en sélectionnant Congé d'arête. Vous pouvez éventuellement appliquer un congé arrondi complet pour créer un mélange homogène d'une ou de plusieurs faces entre deux côtés opposés. -
 Combinaison de faces - Arrondissez des faces intérieures et extérieures tranchantes connectées ou déconnectées pour créer une combinaison homogène entre les faces ou détachez la combinaison pour créer de nouvelles faces, en définissant un rayon ou une largeur constante. Définissez plus en détail la section transversale de la combinaison (bille roulante ou profil balayé), la symétrie, le contrôle, l'ajustement, les contraintes et les limites.
Combinaison de faces - Arrondissez des faces intérieures et extérieures tranchantes connectées ou déconnectées pour créer une combinaison homogène entre les faces ou détachez la combinaison pour créer de nouvelles faces, en définissant un rayon ou une largeur constante. Définissez plus en détail la section transversale de la combinaison (bille roulante ou profil balayé), la symétrie, le contrôle, l'ajustement, les contraintes et les limites. -
 Supprimer la face - Supprimez la géométrie d'une pièce. Choisissez si vous souhaitez corriger les faces environnantes (en les prolongeant jusqu'à ce qu'elles se croisent), fermez ou laissez ouvert. Cet outil de modification directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas avec une pièce importée.
Supprimer la face - Supprimez la géométrie d'une pièce. Choisissez si vous souhaitez corriger les faces environnantes (en les prolongeant jusqu'à ce qu'elles se croisent), fermez ou laissez ouvert. Cet outil de modification directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas avec une pièce importée. -
 Déplacer la face - Translatez, faites pivoter ou décalez une ou plusieurs faces sélectionnées. Cet outil d'édition directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas pour une pièce importée.
Déplacer la face - Translatez, faites pivoter ou décalez une ou plusieurs faces sélectionnées. Cet outil d'édition directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas pour une pièce importée. -
 Remplacer la face - Ajustez ou étendez une face à une nouvelle surface. Cet outil d'édition directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas avec une pièce importée.
Remplacer la face - Ajustez ou étendez une face à une nouvelle surface. Cet outil d'édition directe est particulièrement pratique si vous ne disposez pas de l'historique paramétrique de la pièce, comme c'est souvent le cas avec une pièce importée. -
 Décaler la surface : créez une nouvelle surface en décalant une face, une surface ou une région d'esquisse existante. Définissez la distance de décalage sur 0 pour créer une copie sur place.
Décaler la surface : créez une nouvelle surface en décalant une face, une surface ou une région d'esquisse existante. Définissez la distance de décalage sur 0 pour créer une copie sur place. -
 Surface de contour - Créez ou ajoutez une surface spécifiée par ses profils de contour.
Surface de contour - Créez ou ajoutez une surface spécifiée par ses profils de contour. -
 Remplissage - Créez une surface (ou une pièce à partir de surfaces) en définissant des limites et en affinant la surface avec des conditions aux limites (au lieu de nécessiter l'utilisation de surfaces de référence).
Remplissage - Créez une surface (ou une pièce à partir de surfaces) en définissant des limites et en affinant la surface avec des conditions aux limites (au lieu de nécessiter l'utilisation de surfaces de référence). -
 Déplacer le contour - Déplacez les arêtes de contour d'une surface afin de la prolonger ou de l'ajuster.
Déplacer le contour - Déplacez les arêtes de contour d'une surface afin de la prolonger ou de l'ajuster. -
 Surface réglée - Créez une surface réglée nouvelle ou supplémentaire à partir d'une arête existante ou de plusieurs arêtes d'une zone d'esquisse.
Surface réglée - Créez une surface réglée nouvelle ou supplémentaire à partir d'une arête existante ou de plusieurs arêtes d'une zone d'esquisse. -
 Ajustement mutuel - Ajustez deux surfaces adjacentes en prolongeant les intersections pour terminer l'ajustement.
Ajustement mutuel - Ajustez deux surfaces adjacentes en prolongeant les intersections pour terminer l'ajustement. -
 Surface contrainte - Créez une surface à partir d'une sélection de points ou de données de maillage dans les limites d'une tolérance spécifiée. Affichez les écarts et optimisez les performances ou la fluidité.
Surface contrainte - Créez une surface à partir d'une sélection de points ou de données de maillage dans les limites d'une tolérance spécifiée. Affichez les écarts et optimisez les performances ou la fluidité.
Outre les outils de surfaçage, les courbes sont utilisées pour créer les éléments constitutifs de base des surfaces.
Cette liste répertorie la collection d'outils de fonction de courbes. Elle n'est pas exhaustive. Des outils de fonction supplémentaires peuvent être utilisés lors de la manipulation de courbes.
- Outils d'esquisse : les outils de la barre d'outils d'esquisse, tels que Ligne, Rectangle par sommet, Rectangle à partir du centre, Cercle à partir du centre, Cercle à 3 points, Arc tangent, Arc à 3 points, Spline, Point et Construction, utilisés pour créer une esquisse dans l’Atelier des pièces.
-
 Hélice - Créez une hélice à l'aide d'une face conique ou cylindrique, d'un axe unique ou de l'axe Z d'un connecteur de positionnement, ou d'une arête circulaire.
Hélice - Créez une hélice à l'aide d'une face conique ou cylindrique, d'un axe unique ou de l'axe Z d'un connecteur de positionnement, ou d'une arête circulaire. -
 Spline ajustée en 3D : créez une spline ajustée en 3D à travers une série de sommets. Crée une courbe qui est répertoriée dans la liste des pièces sous Courbes.
Spline ajustée en 3D : créez une spline ajustée en 3D à travers une série de sommets. Crée une courbe qui est répertoriée dans la liste des pièces sous Courbes. -
 Courbe projetée : créez une courbe à partir de la projection de deux esquisses (option Deux esquisses) ou de la projection d'une courbe sur une face (option Courbe à face).
Courbe projetée : créez une courbe à partir de la projection de deux esquisses (option Deux esquisses) ou de la projection d'une courbe sur une face (option Courbe à face). -
 Courbe de jonction : créez une courbe reliant deux points, sommets ou connecteurs de positionnement. La courbe obtenue est répertoriée dans la liste des fonctions et dans la liste des pièces.
Courbe de jonction : créez une courbe reliant deux points, sommets ou connecteurs de positionnement. La courbe obtenue est répertoriée dans la liste des fonctions et dans la liste des pièces. -
 Courbe composite : représente plusieurs arêtes sous la forme d'une seule courbe. Sélectionnez plusieurs arêtes adjacentes, entités d'esquisse et autres courbes. La sélection d'arêtes non contiguës peut entraîner la création de plusieurs courbes. Les sélections pour chaque courbe doivent se rencontrer à leurs sommets. (Les courbes sont répertoriées dans les pièces > Liste des courbes.)
Courbe composite : représente plusieurs arêtes sous la forme d'une seule courbe. Sélectionnez plusieurs arêtes adjacentes, entités d'esquisse et autres courbes. La sélection d'arêtes non contiguës peut entraîner la création de plusieurs courbes. Les sélections pour chaque courbe doivent se rencontrer à leurs sommets. (Les courbes sont répertoriées dans les pièces > Liste des courbes.) -
 Courbe d'intersection : créez une courbe à l'intersection de deux ou plusieurs surfaces ou faces. Les sélections doivent se croiser.
Courbe d'intersection : créez une courbe à l'intersection de deux ou plusieurs surfaces ou faces. Les sélections doivent se croiser. -
 Ajuster la courbe : ajustez ou prolongez une courbe d'une certaine distance ou jusqu'à une entité de délimitation.
Ajuster la courbe : ajustez ou prolongez une courbe d'une certaine distance ou jusqu'à une entité de délimitation. -
 Isocline : créez une isocline sur une face inclinée. Une isocline s'étend sur une face à des positions où la face présente une certaine pente par rapport à sa définition de référence. L'isocline qui en résulte est répertoriée dans la liste des fonctions et la liste des pièces.
Isocline : créez une isocline sur une face inclinée. Une isocline s'étend sur une face à des positions où la face présente une certaine pente par rapport à sa définition de référence. L'isocline qui en résulte est répertoriée dans la liste des fonctions et la liste des pièces. -
 Décaler la courbe : créez et étendez et/ou scindez une nouvelle courbe en décalant les arêtes des faces environnantes.
Décaler la courbe : créez et étendez et/ou scindez une nouvelle courbe en décalant les arêtes des faces environnantes. -
 Courbe isoparamétrique : créez des courbes lisses qui longent une face ou une surface dans la direction U ou V.
Courbe isoparamétrique : créez des courbes lisses qui longent une face ou une surface dans la direction U ou V. -
 Modifier la courbe : modifiez une courbe existante en sélectionnant des entités d'esquisse ou des courbes pour appliquer une approximation simplifiée, augmenter le degré, repositionner les sommets des courbes de contrôle et/ou les planariser dans n'importe quel plan 2D.
Modifier la courbe : modifiez une courbe existante en sélectionnant des entités d'esquisse ou des courbes pour appliquer une approximation simplifiée, augmenter le degré, repositionner les sommets des courbes de contrôle et/ou les planariser dans n'importe quel plan 2D. -
 Courbe de routage - Créez une courbe multipoint sur un ou plusieurs plans dans l'espace 3D (trajectoire routée). Ceci est utile pour créer un routage de tuyauterie, un câblage et des courbes NURBS pour un surfaçage avancé.
Courbe de routage - Créez une courbe multipoint sur un ou plusieurs plans dans l'espace 3D (trajectoire routée). Ceci est utile pour créer un routage de tuyauterie, un câblage et des courbes NURBS pour un surfaçage avancé.
Pour plus de ressources sur le surfaçage, visitez notre centre d'apprentissage.